Previous Next ua

Laboratory Training 4

Use of Functions

1 Training Tasks

1.1 Static Local Variables

Write a program that calculates and outputs the minimum and maximum of integers as the user types those numbers. Two separate functions should be created to find the minimum and maximum, respectively. The previously found minimum and maximum must be stored in static local variables.

In the main() function, you should create a loop in which the user enters an integer, then the functions for finding the minimum and maximum are called, in which the new value is compared with the previously found ones. Output of the functions' result is performed. The loop ends when the user enters zero.

1.2 Recursion

Write a program that reads x and n and calculates y using recursive function:

y = (x + 1)(x + 2)(x + 3)(x + 4) ... (x + n)

1.3 Default Arguments

Create a function with default parameters that returns

1 if no arguments are given,
the value of the argument, if one argument is given,
product of arguments if there are two or three arguments.

Create multiple functions with the same name that return similar results through the name overloading mechanism. The name of these functions must be different from the name of the function with default parameters.

All functions should be tested in the main() function.

1.4 Quadratic Equation

Create a function for solving of quadratic equation. Function should return the number of roots (0, 1, or 2) or -1 if the equation has an infinite number of roots. The function should get the coefficients as arguments and return the roots as reference type arguments. The calculation of the discriminant should be implemented as a local function (via a lambda expression). The function to calculate the discriminant must access the coefficients of the equation through a capture list.

1.5 Individual Assignment

You should create a program that implements an individual assignment of previous laboratory training. Program should be split into several functions. Function y() should obtain values of x and n as arguments and return value calculated using formula given in an individual assignment. Create a separate function for reading data. Do not use global variables.

2 Instructions

2.1 Function Declaration and Definition

2.1.1 The Syntax of Function Declaration and Definition

A function is a subprogram that can act on data and return a value. Each function has its own name. When that name with the list of arguments is encountered, the execution of the program branches to the body of that function. This is called function call, or function invocation. When the function returns, execution resumes on the next line of the calling function. Complicated tasks should be broken down into multiple functions, and then each can be called in turn.

The main() function is called by the operating system.

When calling functions, all their local variables, function addresses, as well as parameter values and other local data are placed in a special memory area called call stack. After return from a function, the area occupied by its local data is freed.

Function definition supplies a function body, the block of code that makes up the function.

The declaration of a function without definition is called its prototype. The function prototype is a function header followed by a semicolon. The function header consists of the function's result type, name, and parameter list. A so-called modifier can be placed in front of the result type, for example, inline. The parameter list is a list of all the parameters and their types, separated by commas.

int sum(int a, int b); // prototype

The function prototype does not need to contain the names of the parameters:

int sum(int, int); // prototype

The function definition consists of the function header and its body. The function prototype and the function definition must agree exactly about the return type, the name, and the parameter list.

int sum(int a, int b)
{
    return a + b;
}

All functions have a return type.

The return statement terminates the function and returns control to the previous function from which the call was made. The result of the main() function can be used by the operating system as an error code (0 - no errors).

The value of expression in return statement is returned to the calling function. Functions of all types (except void) must specify an expression in the return statement.

The return statement always terminates the function.

Although there is no limit to the size of a function in C++, well-designed functions tend to be small. A smaller function is easier to understand and maintain.

2.1.2 Calling Functions

The arguments are passed in to the function in the order in which they are declared and defined. Any valid C++ expression can be a function argument, including constants, mathematical and logical expressions, and other functions that return a value.

int main()
{
    int x, y;
    cin >> x >> y;
    int z = sum(x, y);             // function call
    int k = sum(z, x + y);         // function call
    int m = sum(k, sum(x + y, z)); // function call
    int m = sum(3, 4);             // function call
    cout << z << ' ' << k << ' ' << m << ' ' << n;
    return 0;
}

The arguments passed into the function are local to the function. Changes made to the arguments do not affect the values in the calling function. This is known as passing by value, which means a local copy of each argument is made in the function.

Calling programs pass information to called functions in actual arguments. The called functions access the information using corresponding formal arguments.

2.1.3 The void Returning Type

If a function does not return a value, its return type will be void.

void print(double a)
{
    cout << a << endl;
}

The void type is syntactically a fundamental type. It can, however, be used only as part of a more complicated type; there are no objects of type void.

If a function returns void, the body of function is executed until the end of programming block. Functions of type void cannot specify expressions in the return statement. In such functions you can use return statement without expression to terminate the execution of a function. For example

void printReciprocal(double a)
{
    if (a == 0)
    {
        return;
    }
    cout << 1 / a << endl;
}

A function with the void result type can only be called using a separate statement (not inside an expression).

int main()
{
    int x;
    cin >> x;
    printReciprocal(x); // function call
    return 0;
}

2.1.4 Allocation of Functions in the Program

The traditional scheme of compiling program code in C++ involves the sequential translation of statements without searching for undeclared names further down the text. Everything we use must be defined or announced beforehand. This also applies to functions. In order for a function to be called, its definition (or prototype) must be located before the call. In programs that use functions, the function that we call must be placed before the function from which the call is made:

#include <iostream>
using namespace std;

int sum(int a, int b)
{
    return a + b;
}

int main()
{
    int n = sum(3, 4);
    cout << n;
    return 0;
}

An alternative option is to place a prototype (or prototypes) before the main() function. Then the functions that we call can be placed after the main() function:

#include <iostream>
using namespace std;

int sum(int, int);

int main()
{
    int n = sum(3, 4);
    cout << n;
    return 0;
}

int sum(int a, int b)
{
    return a + b;
}

Prototypes can be repeated many times, and can also be placed inside the body of a function:

#include <iostream>
using namespace std;

int main()
{
    int sum(int, int);
    int n = sum(3, 4);
    cout << n;
    return 0;
}

int sum(int a, int b)
{
    return a + b;
}

2.1.5 Local Functions and Lambda Expressions

A function can be defined inside another function. In C++, an alternative syntax is used to define local functions - so-called lambda expressions, which appeared in C++ starting with the C++11 language standard. Lambda expressions are expressions for representing functions inside code. The term "lambda" was taken from the mathematical theory of recursive functions, where the letter λ was used to denote a function. The syntax of a lambda expression in C++ looks like this:

[capture list] (parameter list) { function body }

You can include local variable names or external function parameters in the capture list. The capture list and parameter list can be empty. Below is an example of the simplest lambda expression:

[](){ cout << "Hello, world!" << endl; }

In the simplest case, a lambda expression can be used as a regular function:

[](){ cout << "Hello, world!" << endl; }();
cout << [](int a, int b) { return a * b; }(2, 2); // 4

You can create a variable that can be used to call:

auto f = [](int a, int b) { return a * b; };
cout << f(2, 2); // 4

A local function with two parameters is actually created.

The resulting type of expression depends on the invocation context. Sometimes, you need to specify type explicitly. You can do that by placing In the arrow operator followed by the return type between the parameter list and the function body. In the following example the result is converted to int type:

auto g = [](double a, double b) -> int { return a + b; };
cout << g(2.2, 2.3); // 4

The use of local functions can be demonstrated on the example of calculating the distance between two points using the following formula:

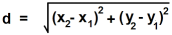
The standard library provides a function for calculating the square root. For calculating the second power you can use the pow() function, which is generally inefficient, or multiplying the value by itself, which is not always convenient. We can create a local function for calculating the second power. The program will be as follows:

#include <iostream>
using namespace std;

double distance(double x1, double y1, double x2, double y2)
{
    auto sq = [](double a) { return a * a; };
    return sqrt(sq(x2 - x1) + sq(y2 - y1));
}

int main()
{
    cout << distance(1, 1, 4, 5) << endl;
    return 0;
}

The following example demonstrates the use of a capture list. The function outputs the values of the parameters, then the parameters are replaced by their return values, and we want to get changed parameters.

#include <iostream>
using namespace std;

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printParams();
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    printParams();
}

int main()
{
    printReciprocalValues(3, 4, 5);
}

Capturing is done once. So, identical values will be output twice:

3 4 5
3 4 5

In order to output the changed values, it is necessary to define another local function and perform a new capture. The code of printReciprocalValues() function will now look like this:

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printParams();
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    auto printModified = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printModified();
}

Now the result will be different:

3 4 5
0.333333 0.25 0.2

In order to use the only function, instead of a capture list, you should use a parameter list:

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [](double a, double b, double c) { cout << a << " " << b << " " << c << "\n"; };
    printParams(a, b, c);
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    printParams(a, b, c);
}

Starting with C++11, a syntax similar to lambda expressions (without the capture list) can be used to describe regular functions. For example, instead of declaring a function

int sum(int a, int b);

you can write:

auto sum(int a, int b) -> int;

The corresponding headers can be used when implementing the function.

auto sum(int a, int b) -> int
{
    return a + b;
}

From a practical point of view, this syntax for ordinary (non-local) functions offers no advantages.

2.2 Scope

2.2.1 Overview

A variable has scope, which determines how long it is available to the program and where it can be accessed.

You can declare variables within the body of the function, or other program block. This can be done using local variables. Such variables exist only locally within the function itself. The parameters passed in to the function are also considered local variables.

Global variables have global scope. They are available anywhere within your program. The global variables defined outside any function are available from any function in the program, including main(). Local variables with the same name as global variables do not change the global variables. A local variable with the same name as a global variable hides the global variable. However, you can use scope resolution operator (::) for access to global variable. For example

int k = 1;

void f()
{
    int k = 2;
    cout << k;   // 2
    cout << ::k; // 1
}

In C++, global variables are legal, but their usage is not recommended. Global variables are dangerous because they are shared data. One function can change a global variable in a way that is invisible to another function. This can produce bugs that are difficult to find.

Local blocks can be created inside the block that defines the function body. You can create your own local variables in them. In C++, you can define names in an inner block that are already defined in an outer block:

{
    int i = 0;
    {
        int i = 2; // new variable
    }
}

Now the variable i is not accessible from the inner block. There are no syntactic constructs that can provide such access. Such definitions lead to non-obvious errors. Such structures should be avoided.

2.2.2 Static Local Variables

Normally, variables defined local to a function disappear at the end of the function scope. When you call the function again, storage for the variables is created anew and the data is reinitialized. If you want the data to be extant throughout the life of the program, you can define that variable to be static and give it an initial value. The initialization is only performed when the function invokes for the first time, and the data retains its value between function calls. The following example demonstrates the difference between normal (automatic) and static local variables:

#include <iostream>

using namespace std;

void localVariables()
{
    int m = 0;
    static int n = 0;
    m++;
    n++;
    cout << m << " " << n << endl;
}

int main()
{
    localVariables(); // 1 1
    localVariables(); // 1 2
    localVariables(); // 1 3
    return 0;
}

Although static variables exist throughout the program's life cycle, there are no mechanisms for accessing such variables from outside the function, so they can't be inadvertently changed. This reduces the possibility of errors.

2.3 Recursion

A function can call itself. This is called recursion.

Recursion can be direct or indirect. It is direct recursion when a function calls itself:

void f() {
    ...
    f();
    ...
}

It is important to note that when a function calls itself, a new copy of that function is run. The local variables in the second version are independent of the local variables in the first, and they cannot affect one another directly.

The misuse of recursion can cause stack overflow error.

Sometimes you can use recursion instead of looping. But you should keep in mind that most of the tasks of recursion reduce efficiency through and creates difficulty in deprivation.

The use of recursion is advisable in the tasks of bypassing the tree-shaped data structures, in particular, the subdirectories of the file system.

For example, you can calculate sum

y = 1² + 2² + 3² + ... + n²

without any loop:

#include <iostream>

using namespace std;

double sum(int n)
{
    if (n <= 1)
    {
        return 1;
    }
    else
    {
        return n * n + sum(n - 1);
    }
}

int main()
{
    cout << sum(5);
    return 0;
}

In general, this approach is not desirable, makes the code less comprehensible, and can lead to errors.

Indirect recursion means that the first function calls the second function, and then the second function calls the first function. In this case, it is necessary to create a prototype of at least one of the functions:

void f(); // prototype
void g() {
    ...
    f();
    ...
}
void f() {
    ...
    g();
    ...
}

Indirect recursion can be used to simplify the implementation of some algorithms. For example, it can be used to find prime numbers:

#include <iostream>
using namespace std;

unsigned int nextPrime(unsigned int); // prototype

// Checks either a number is prime
bool isPrime(unsigned int number)
{
    unsigned int prime = 2; // first prime number
    // Checks until the square root of number, whether number is divisible by some prime number:
    while (prime * prime <= number && number % prime != 0)
    {
        prime = nextPrime(prime);
    }
    return number % prime; // true if not divided
}

// Finds the next prime after the given number
unsigned int nextPrime(unsigned int number)
{
    unsigned int prime = number + 1;
    while (!isPrime(prime))
    {
        prime++;
    }
    return prime;
}

int main()
{
    unsigned int n;
    cout << "Enter a positive integer: ";
    cin >> n;
    cout << "The number is " << n << (isPrime(n) ? " " : " not ") << "prime.\n";
    cout << "The next prime after " << n << " is " << nextPrime(n);
    return 0;
}

This algorithm, of course, is not the most efficient, but it provides a relatively transparent implementation.

2.4 Inline Functions

When a function is called, program execution jumps to the corresponding instructions. When the execution of the function completes, execution jumps back to the next line of the function from which the call was made. These actions may be associated with some reduction in performance.

There are so-called inline functions, or built-in functions. Such functions have an inline modifier:

inline int min(int a, int b)
{
    return a < b ? a : b;
}

The inline specifier instructs the compiler to insert a copy of the function body into each place the function is called. If the function is very small, no more than a line or two, and won't be called from many places in your program, it is a candidate for inlining.

An inline function cannot be recursive. If you add the inline modifier to the header of such a function, it will be ignored by the compiler.

Modern compilers try to convert all functions into inline functions if possible and increase the performance of the program. However, the explicit use of the inline modifier allows the function to be defined multiple times, which is important from the point of view of the location of such definitions in the header files.

2.5 Function Name Overloading

C++ enables you to create more than one function with the same name. This is called function name overloading. Overloaded functions enable programmers to supply different semantics for a function, depending on the types and number of arguments.

The functions must differ in their parameter list, with a different type of parameter, a different number of parameters, or both. Here's an example:

int sum(int a, int b)
{
    return a + b;
}

double sum(double a, double b)
{
    return a + b;
}

double sum(double a, double b, double c)
{
    return a + b + c;
}

int main()
{
    cout << sum(1, 2) << endl;      // first  sum() function
    cout << sum(1.0, 2.5) << endl;  // second sum() function
    cout << sum(1, 2, 2.6) << endl; // third  sum() function
    return 0;
}

You should note that two functions with the same name and parameter list, but different return types, generate a compiler error:

int f(double x);
double f(double x); // Error

2.6 Default Arguments

In many cases, functions have arguments that are used so infrequently that a default value would suffice. To address this, the default-argument facility allows for specifying only those arguments to a function that are meaningful in a given call. Here's an example:

int sum(int x, int y = 0, int z = 0)
{
    return x + y + z;
}

int main()
{
    cout << sum(5) << endl;       // 5, y = 0, z = 0
    cout << sum(1, 2) << endl;    // 3, z = 0
    cout << sum(1, 2, 5) << endl; // 8
    return 0;
}

Default arguments will be used in calls where trailing arguments are missing. Any or all of the function's parameters can be assigned default values. The one restriction is this: If any of the parameters does not have a default value, no previous parameter may have a default value. Default arguments must be the last arguments:

void f(double x, int y = 0, int h); // Error.

A default argument cannot be redefined in later declarations even if the redefinition is identical to the original. Therefore, the following code produces an error:

void f(double x, int y = 1);
void f(double x, int y = 1) { } // Error. 
  // Must be void f(double x, int y) { }

2.7 References

2.7.1 Overview

The C++ language defines a mechanism for creating so-called references. A reference can be defined as a second name (alias) of an existing variable (object).

You can declare a reference by writing the type, followed by the reference operator (&), followed by the reference name.

int i = 10; 
int &j = i; // reference to i
j = 11;
cout << i;  // 11

As an alias cannot exist without its corresponding real part, you cannot define single references. References must be initialized at the time of creation.

int &k; // Syntax error!

There are no constant references, but you can declare references to constant objects:

int m = 2; 
const int &n = m; // reference to m
double x = n + 1; // OK
m = 11;           // OK 
n = 12;           // error!

2.7.2 References as Function Arguments

References can be used as function arguments. Suppose you want to create a function that exchanges the values of two integer variables. The first version of the function will be:

void swap(int x, int y)
{
    int z = x;
    x = y;
    y = z;
}

You can try to call this function, but unfortunately, the values of the variables are not changed, while the values of x and y in the swap() function have changed (you can check with the debugger)

void swap(int x, int y) // x = 1, y = 2
{
    int z = x;
    x = y;
    y = z; // x = 2, y = 1
}

int main()
{
    int a = 1;
    int b = 2;
    swap(a, b);
    cout << a << endl; // 1
    cout << b << endl; // 2
    return 0;
}

The problem is that the changed values of the parameters are not copied back to the main() function.

Using references will help to solve this problem. If you describe parameters as references, the synonyms for the variables that are passed as actual parameters are created:

void swap(int &x, int &y)
{
    int z = x;
    x = y;
    y = z;
}

In fact, in the function we work with the same variables that we created in the main() function:

int main()
{
    int a = 1;
    int b = 2;
    swap(a, b);
    cout << a << endl; // 2
    cout << b << endl; // 1
    return 0;
}

Reference type parameters can also be used to return multiple results from a function. For example, it is necessary to solve the following equation:

|x| – b = 0

Since there are two roots, it is advisable to use link parameters:

#include <iostream>
using namespace std;

void solveEquation(double b, double& x1, double& x2)
{
    x1 = b;
    x2 = -b;
}

int main()
{
    double b, x1, x2;
    cin >> b;
    solveEquation(b, x1, x2);
    cout << "x1 = " << x1 << " x2 = " << x2;
    return 0;
}

2.7.3 Passing a Reference to a Constant Object

Passing parameters by reference can also be used to pass large objects to a function (structures and classes will be discussed later). Instead of copying the object through the call stack, it is sufficient to pass its address, as is done for references. But at the same time, there is a danger of accidentally changing the value of the object, because in the function we continue to work with the same object as in the place of the call. Also, constants cannot be sent as parameters. In such cases, you can use a reference to a constant object. It is impossible to change the value of such a parameter in the function body.

For example, we need to find the third power of a number of type double. We pass the number by reference with the const modifier. Inside the body of the function, it is forbidden to change the value of the following parameter:

double cube(const double &x)
{
    double y = x * x * x;
    x = 3; // error!
    return y;
}

After fixing the error, we can use this function, including for constant parameters and expressions, because constants are also located in memory and have an address:

#include <iostream>
using namespace std;

double cube(const double &x)
{
    double y = x * x * x;
    return y;
}

int main()
{
    double x = 4;
    const double c = 3;
    cout << cube(x) << endl;
    cout << cube(c) << endl;
    cout << cube(1.6) << endl;
    cout << cube(6 - 4) << endl;
    return 0;
}

2.7.4 Reference as a Result of a Function

References can be used as return values. It is very important to ensure that the reference is bound with the variable that exists after leaving a function:

int& f()
{
    int k;
    return k; // Error; k is destroyed after leaving a function
}

That's correct:

int& f()
{
    static int k;
    return k; // OK
}

int main()
{
    f() = 10;
    cout << f(); // 10
    return 0;
}

A function returns an alias to static variable that is not destroyed after leaving a function. Therefore, we can assign

f() = 10; // k = 10

We assign the value not to the function, but to its result - to the variable, the reference to which the function returns.

A function that returns a reference can be used, for example, so that a group of variables can be accessed in a loop:

#include <iostream>
using namespace std;

double x, y, z;

double& variable(int k)
{
    switch (k)
    {
        case 1:  return x;
        case 2:  return y;
        default: return z;
    }
}

int main()
{
    for (int i = 1; i <= 3; i++)
    {
        variable(i) = i;
    }
    cout << x << " " << y << " " << z; // 1 2 3
    return 0;
}

It is important that the function always should always return the reference to any variable, so it is advisable to return the reference to z for any value, not just 3.

2.8 Structure of a Program that Uses Functions

The easiest way to use functions in the program is to select separate parts related to specific information processing algorithms. Such parts must have a fixed set of source data, a fixed set of results, and be independent of the code of other functions. Global variables can be used for information exchange in function code, but the use of such variables should be minimized.

Almost every program can be divided into relatively independent parts. Program that calculates some values usually contains parts responsible for input, calculation, and output. Assume that we need to implement a program that calculates sum of second powers of integers:

y = 1² + 2² + 3² + ... + n²

The first implementation is not divided into parts:

#include <iostream>

using namespace std;

int main()
{
    int n;
    cout << "Input n:";
    cin >> n;
    int y = 0;
    for (int i = 1; i <= n; i++)
    {
        y += i * i;
    }
    cout << "y = " << y;
    return 0;
}

The simplest solution of dividing into separate functions consists in use of global variables:

#include <iostream>

using namespace std;

int n;
int y = 0;

void read()
{
    cout << "Input n:";
    cin >> n;
}

void calc()
{
    for (int i = 1; i <= n; i++)
    {
        y += i * i;
    }
}

void write()
{
    cout << "y = " << y;
}

int main()
{
    read();
    calc();
    write();
    return 0;
}

Use of global variables is not a good idea. The better approach consists in use of arguments:

#include <iostream>

using namespace std;

int read()
{
    int n;
    cout << "Input n:";
    cin >> n;
    return n;
}

int calc(int n)
{
    int y = 0;
    for (int i = 1; i <= n; i++)
    {
        y += i * i;
    }
    return y;
}

void write(int y)
{
    cout << "y = " << y;
}

int main()
{
    int n = read();
    int y = calc(n);
    write(y);
    return 0;
}

The main() function can be implemented without any variables.

...

int main()
{
    write(calc(read()));
    return 0;
}

The functions that are parts of a large program should not be very long, for example, up to 20 lines of code, otherwise it is better divided into several functions.

It is important that a function that is designed to return a result does not simultaneously output that result to the console, unless it is determined by the task. Suppose, for example, that we need to create a function that calculates the third power of a number, and then print the result. Instead of combining calculation and output in one function

double cube(double x)
{
    double y = x * x * x;
    cout << y;
    return y;
}

it is better to implement output in main() function, or create a separate function for output:

double cube(double x)
{
    return y = x * x * x;
}

void printCube(double x)
{
    cout << cube(x);
}

A function that only returns the result, rather than output to the console, can be more universal: it can be called many times in expressions, and it can be used not only in console applications. It is better to pass the necessary data as parameters.

2.9 Use of Standard Functions

Before implementing data processing algorithms, in particular, creating custom functions, it is advisable to make sure that these algorithms are not implemented by standard functions.

In order to use the standard function in the program, it is necessary to include the header file, which contains the declaration (prototype) of the corresponding function. The header files with the corresponding functions are located in the include folder and are supplied together with the compiler, linker and other tools for creating C++ programs. The implementation of functions in a compiled form is allocated in files with the .lib extension. If the programming environment was installed correctly, there is no need to search for these files. The compiler and linker are aware of their location.

In addition to function declarations, the necessary types and constants are located in the header files.

The cmath header file contains declarations of mathematical functions. The table shows the most used mathematical functions:

Function	Meaning	Example
`double pow(double a, double b)`	Calculation of a^b	`pow(x, y)`
`double sqrt(double a)`	Calculation of square root	`sqrt(x)`
`double sin(double a)`	Calculation of sine	`sin(x)`
`double cos(double a)`	Calculation of cosine	`cos(x)`
`double tan(double a)`	Calculation of tangent	`tan(x)`
`double asin(double a)`	Calculation of arc sine	`asin(x)`
`double acos(double a)`	Calculation of arc cosine	`acos(x)`
`double atan(double a)`	Calculation of arc tangent	`atan(x)`
`double exp(double a)`	Calculation of e^x	`exp(x)`
`double log(double a)`	Calculation of natural logarithm (base e)	`log(x)`
`int``abs(int a)``double` `abs(double a)`	Obtaining of the absolute value	`abs(x)`
`double` `fabs(double a)`	Obtaining of the absolute value	`fabs(x)`
`long round(double a)`	Obtaining of the closest integer value	`round(x)`

For trigonometric functions, the argument is specified in radians.

The following example demonstrates the operation of mathematical functions:

#include <iostream>
using namespace std;

int main()
{
    double x = 2;
    cout << pow(x, 4) << endl; // 16
    cout << sqrt(x)   << endl; // 1.41421
    cout << sin(x)    << endl; // 0.909297
    cout << cos(x)    << endl; // -0.416147
    cout << tan(x)    << endl; // -2.18504
    cout << asin(x)   << endl; // -nan(ind), math error
    cout << atan(x)   << endl; // 1.10715
    cout << exp(x)    << endl; // 7.38906
    cout << log(x)    << endl; // 0.693147
    x = -2.8;
    cout << abs(x)    << endl; // 2.8
    cout << round(x)  << endl; // -3
    return 0;
}

The ctime header file ctime allows you to work with times and dates. The time() function returns the time as seconds elapsed since midnight, January 1, 1970, or -1 if there's an error.

For example, you can get the current time in this way:

long long currentTime = time(NULL);

The clocale header file provides setlocale()function that allows setting the specified system locale. For example, we use the following function call to set ukrainian localization:

setlocale(LC_ALL, "UKRAINIAN");

Standard header files often contain the inclusion of other files. For example, the iostream header file iostream contains the inclusion of clocale.

Prototypes for some of the most universal functions can be found in the cstdlib header file. For example, so-called random numbers are often used to test programs related to calculations. The value of a random number cannot be predicted in advance, but it is possible to estimate the probability of a value, or obtaining a number from a certain range. The simplest case is the so-called uniformly distributed numbers: the probability of occurrence of each individual value within the range is the same. They often work with random values of an integer type. If you get numbers like this long enough, each value from the selected range will appear about the same number of times.

To obtain random integers, we use the rand() function:

int rand();

The rand() function returns an integer value between 0 and 32767 inclusive. If we need to get numbers from a smaller range, it is advisable to use the remainder from division. For example, the program generates numbers in the range from 0 to 9 inclusive:

#include <cstdlib>
#include <iostream>

using namespace std;

int main()
{
    for (int i = 0; i < 100; i++)
    {
        int k = rand() % 10;
        cout << k << " ";
    }
    return 0;
}

The rand() function generates so-called pseudo-random numbers. Although they are evenly distributed over the specified range, the sequence of numbers is repeated each time the program is launched. We get so-called pseudo-random numbers. The generation of such numbers is carried out starting from a certain initial integer value. This number can be specified using a srand() function with an integer parameter. By determining different values each time, you can get different sequences of pseudorandom numbers.

In order to obtain true random numbers, the generator should be initialized with a truly random number. The number of seconds returned by the time() function will of course be different each time, so the sequence of numbers will be new each time and now the numbers will be truly random. Our previous program that will generate random numbers will look like this:

#include <cstdlib>
#include <ctime>
#include <iostream>

using namespace std;

int main()
{
    srand(time(NULL));
    for (int i = 0; i < 100; i++)
    {
        int k = rand() % 10;
        cout << k << " ";
    }
    return 0;
}

The cstdlib header file also contains declaration of a system() function. The parameter of this function is a string that contains a specific command of the operating system. It can be a built-in kernel command of the operating system, a standard utility, or even a program previously created by the user.

For example, when working under a Windows operating system, you can clear the console window like this:

system("cls");

It is possible to delay the program execution until pressing any key:

system("pause");

You can launch any program, for example, notepad:

system("notepad");

You can also set the required code page for the console application to run. For example, this is how you can set the Cyrillic code page:

system("chcp 1251");

After setting the page, the message "Active code page: 1251" appears in the console window. To suppress the appearance of this message, it can be resent to a file, or to the object called nul (nothing):

system("chcp 1251 > nul");

The cstring header file provides function prototypes for working with null-terminated strings. The cstdio header file contains function declarations that implement C-style input and output (e. g, scanf(), printf() etc.). The functions of these header files will be discussed later.

All standard library functions are defined in the std namespace.

3 Sample Programs

3.1 The Sum of Successive Powers of a Number

In the following program the user enters the value of x and the integer n. It is necessary to calculate the sum of successive integer powers x from 1 to n.

#include <iostream>

using namespace std;

double sumOfPowers(double x, int n)
{
    double sum = 0;
    double power = 1;
    // Powers and the sum can be calculated in a single loop:
    for (int i = 0; i < n; i++)
    {
        power *= x;
        sum += power;
    }
    return sum;
}

int main()
{
    double x;
    int n;
    cout << "Enter x and n:";
    cin >> x >> n;
    cout << sumOfPowers(x, n);
    return 0;
}

3.2 Static local variable

This program calculates and shows the sum of integers as the user inputs those integers.

#include <iostream>

using namespace std;

int add(int i)
{
    static int sum = 0;
    sum += i;
    return sum;
}

int main()
{
    int i;
    do
    {
        cin >> i;
        cout << add(i) << endl;
    }
    while (i);
    return 0;
}

3.3 Linear Equation

Function solve() in the following example finds root of a linear equation (the argument passed by reference) and returns the number of roots. If the number of roots is infinite, the function returns -1. Inside the main() function, it is advisable to create a switch that analyzes the number of roots and performs the appropriate output

#include <iostream>

using namespace std;

int solve(double a, double b, double& x)
{
    if (a == 0)
    {
        if (b == 0)
        {
            return -1;
        }
        else
        {
            return 0;
        }
    }
    x = -b / a;
    return 1;
}

int main()
{
    double a, b, x;
    cin >> a >> b;
    int count = solve(a, b, x);
    switch (count)
    {
    case -1:
        cout << "Infinite number of roots";
        break;
    case 0:
        cout << "No roots";
        break;
    case 1:
        cout << "x = " << x;
    }
    cout << endl;
    return 0;
}

3.4 Function Values Table

Suppose we need to create a program that calculates the values of a function on a given range with a certain step

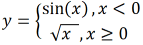
Individual parts of the program should be implemented as independent functions. The program can be as follows:

#include <iostream>
#include <cmath>
using namespace std;

// Data input from the keyboard, parameters are transferred by the reference
bool readData(double& from, double& to, double& step)
{
    cout << "Enter the beginning, end of the interval, and step: ";
    cin >> from >> to >> step;
    if (from >= to || step <= 0)
    {
        cerr << "Wrong data" << endl;
        return false;
    }
    return true;
}

// The function defined in the task
double y(double x)
{
    if (x < 0)
    {
        return sin(x);
    }
    else
    {
        return sqrt(x);
    }
}

// Output of values of arguments and functions on an interval with the certain step
void printInALoop(double from, double to, double step)
{
    cout << "x\ty" << endl; // table header
    for (double x = from; x <= to; x += step)
    {
        cout << x << "\t" << y(x) << endl;
    }
}

int main()
{
    double from, to, step;
    if (readData(from, to, step))
    {
        printInALoop(from, to, step);
        return 0; // OK
    }
    return -1; // data input error
}

The location of functions in the program is determined by the call mechanism. The function that is called must precede the function that calls it. This order is not always convenient in terms of human perception of the code. If we first place function prototypes, we can change the order:

#include <iostream>
#include <cmath>
using namespace std;

// Function prototypes:
bool readData(double &, double &, double &);
void printInALoop(double, double, double);
double y(double);

int main()
{
    double from, to, step;
    if (readData(from, to, step))
    {
        printInALoop(from, to, step);
        return 0; // OK
    }
    return -1; // data input error
}

// Data input from the keyboard, parameters are transferred by the reference
bool readData(double& from, double& to, double& step)
{
    cout << "Enter the beginning, end of the interval, and step: ";
    cin >> from >> to >> step;
    if (from >= to || step <= 0)
    {
        cerr << "Wrong data" << endl;
        return false;
    }
    return true;
}

// Output of values of arguments and functions on an interval with the certain step
void printInALoop(double from, double to, double step)
{
    cout << "x\ty" << endl; // table header
    for (double x = from; x <= to; x += step)
    {
        cout << x << "\t" << y(x) << endl;
    }
}

// The function defined in the task
double y(double x)
{
    if (x < 0)
    {
        return sin(x);
    }
    else
    {
        return sqrt(x);
    }
}

3.5 Creating Functions to Work with the State of the Program

In the following example, the values of constants (flags) are consecutive powers of 2, setFlag(), removeFlag() and clearState() functions change the state of the program (global variable). The printBinary() function outputs the values in the binary notation. The program demonstrates the change and analysis of the state:

#include <iostream>

using std::cout;

const unsigned char NO_DATA = 0;
const unsigned char DATA_READ = 1;
const unsigned char SOLVED = 2;
const unsigned char ROOTS_FOUND = 4;

unsigned char state = 0;

void setFlag(unsigned char flag)
{
    state |= flag;
}

void removeFlag(unsigned char flag)
{
    state &= ~flag;
}

bool checkState(unsigned char flag)
{
    return state & flag;
}

void clearState()
{
    state = NO_DATA;
}

void printBinary(unsigned char flag)
{
    const int size = sizeof(flag) * 8;
    for (int i = 0; i < size; i++)
    {
        cout << (flag >> (size - 1));
        flag <<= 1;
    }
    cout << "\n";
}

int main()
{
    cout << "Flags:\n";
    printBinary(NO_DATA);
    printBinary(DATA_READ);
    printBinary(SOLVED);
    printBinary(ROOTS_FOUND);

    cout << "Initial state\n";
    printBinary(state);

    cout << "Data entered\n";
    setFlag(DATA_READ);
    printBinary(state);

    cout << "Data cleared\n";
    removeFlag(DATA_READ);
    printBinary(state);

    cout << "Data entered again\n";
    setFlag(DATA_READ);
    printBinary(state);

    if (checkState(DATA_READ)) {
        std::cout << "Equation was solved\n";
        setFlag(SOLVED);
        printBinary(state);
        setFlag(ROOTS_FOUND);
        printBinary(state);
    }
    std::cout << "We start first\n";
    clearState();
    printBinary(state);
    return 0;
}

The results of the program work will be as follows :

Flags:
00000000
00000001
00000010
00000100
Initial state
00000000
Data cleared
00000001
Data cleared
00000000
Data entered again
00000001
Equation was solved
00000011
00000111
We start first
00000000

4 Exercises

Create a program that tests signum() function.
Develop and test a function that calculates product of three arguments.
Develop and test a function that calculates product of n first odd values.
Develop and test a function that calculates e^x using sum.
Develop and test a function that calculates factorial.
Develop and test a function that prints all even values in a given range.
Develop and test a function and prints product of n first even values.
Develop and test a function that calculates greatest common divisor of two integers.

5 Quiz

What is function?
What is function header?
What is function body?
What is a function prototype?
How to create a local function?
What is a capture list?
How are parameters passed to a function?
What is the difference between actual arguments and formal arguments?
Is return statement always obligatory?
Can a function with a void result type contain a return statement?
What is a local variable?
What is scope?
What is global scope?
How to access names from global scope?
Can local variables hide global variables?
What is the difference between static and non-static local variables?
What is lifecycle of static local variable?
How to use static local variables?
What is recursion?
What is inline function?
How to overload function name?
Can you create two global functions with the same name and parameter list, but different return types?
How to declare default arguments?
What are references?
How to initialize reference?
What is the usage of references?
What is a reference to a constant object used for?
Can you return a reference from a function?
Can you return a reference to non-static local variable?
What is a random and pseudo-random number? How to get random numbers?

Previous Next

Fundamentals of Programming (Part 1) / Algorithmization and Programming (Part 1)

Developed by Leo V. Ivanov

Laboratory Training 4 – Use of Functions