Основи програмування (частина 1)

Розробник курсу Л. В. Іванов

Лабораторна робота 4 – Використання функцій

Попередня Наступна en

Лабораторна робота 4

Використання функцій

1 Завдання на лабораторну роботу

1.1 Статичні локальні змінні

Написати програму, яка обчислює та виводить мінімум і максимум цілих чисел, в міру того, як користувач вводить ці числа. Слід створити дві окремих функції для знаходження мінімуму і максимуму відповідно. Попередньо знайдені мінімум і максимум повинні зберігатися в статичних локальних змінних.

У функції main() слід створити цикл, в якому користувач уводить ціле число, після чого викликаються функції для знаходження мінімуму і максимуму, в яких нове значення порівнюється з попередньо знайденими. Здійснюється виведення результату функцій. Цикл завершується, коли користувач уводить нуль.

1.2 Рекурсія

Написати програму, яка зчитує x і n і обчислює y за допомогою рекурсивної функції:

y = (x + 1)(x + 2)(x + 3)(x + 4) ... (x + n)

1.3 Аргументи з усталеними значеннями

Створити функцію з усталеними значеннями параметрів, яка повертає

  • значення 1, якщо аргументи не задані,
  • значення аргументу, якщо задано один аргумент,
  • добуток аргументів якщо аргументів два чи три.

Створити декілька функцій з однаковим ім'ям, які повертають аналогічні результати через механізм перевантаження імен. Ім'я цих функцій повинно відрізнятися від імені функції з усталеними значеннями параметрів.

У функції main() слід здійснити тестування всіх функцій.

1.4 Квадратне рівняння

Створити функцію для розв'язання квадратного рівняння. Функція повинна повертати кількість коренів (0, 1 або 2) або -1, якщо рівняння має безліч розв'язків. Функція повинна отримати коефіцієнти як аргументи та повертати корені як аргументи-посилання. Обчислення дискримінанта слід реалізувати як локальну функцію (через лямбда-вираз). Функція для обчислення дискримінанта повинна отримувати доступ до коефіцієнтів рівняння через список захоплення.

1.5 Індивідуальне завдання

Створити програму, яка реалізує індивідуальне завдання попередньої лабораторної роботи. Програма повинна бути розділена на декілька функцій. Функція y() повинна отримувати значення x і n як аргументи й повертати значення, розраховані за формулою, наведеною в індивідуальному завданні. Створити окрему функцію для зчитування даних. Не використовувати глобальні змінні.

2 Методичні вказівки

2.1 Оголошення та визначення функції

2.1.1 Синтаксис оголошення та визначення функції

Функція (function) – це підпрограма, яка може отримати дані та повертати деяке значення. Кожна функція має своє власне ім'я. Коли це ім'я зі списком даних (параметрів) зустрічається будь-де у програмі, виконання програми переходить до тіла цієї функції. Такий перехід має назву виклику функції (function call). Після того, як були виконані інструкції в тілі функції, процес виконання повертається до попередньої функції (з якої було здійснено виклик) та виконуються її наступні інструкції. Складні програми повинні бути розділені на декілька функцій, виклик яких здійснюється по черзі.

Виклик функції main() здійснюється операційною системою.

Під час виклику функцій усі їх локальні змінні, адреси функцій, а також значення параметрів і інші локальні дані розміщуються в спеціальній області пам'яті, що зветься програмним стеком, або стеком викликів (call stack). Під час повернення з функції область, зайнята її локальними даними, звільняється.

Визначення функції включає тіло функції (function body) – блок з програмним кодом, який виконується під час виклику функції.

Оголошення функції без визначення має назву прототипу (prototype). Прототип функції – це заголовок функції, після якого розташована крапка з комою. Заголовок функції складається з типу результату функції, імені та списку параметрів. Перед типом результату може бути розташований так званий модифікатор, наприклад, inline. Список параметрів(parameter list) – це список всіх аргументів та їх типів, розділених комами.

Це прототип функції, яка обчислює та повертає суму двох цілих чисел:

int sum(int a, int b); // прототип

Прототип функції не обов'язково містить імена параметрів:

int sum(int, int); // прототип

Визначення функції (function definition) складається з заголовка функції й тіла. Прототип функції та визначення функції повинні збігатися щодо типу результату, імені та списку параметрів.

int sum(int a, int b)
{
    return a + b;
}

Усі функції мають тип результату.

Інструкція return завершує виконання функції та повертає управління до попередньої функції, з якої було здійснено виклик. Інструкція returnвсередині функції main() передає управління операційній системі, а результат, який повертає функція main(), може бути використаний як код помилки (0 - помилок немає).

Значення виразу в інструкції return повертається до функції, з якої було здійснено виклик. Функції усіх типів (за винятком типу void) повинні містити інструкцію return з таким виразом.

Інструкція return завжди завершує виконання функції.

Попри те, що немає обмеження на розмір функції, добре спроєктовані функції зазвичай містять не дуже багато коду. Функцію з меншим розміром легше зрозуміти та підтримувати її роботу.

2.1.2 Виклик функцій

Аргументи передаються у функцію в тому порядку, в якому вони були оголошені й визначені. Будь-який вираз C++ може бути аргументом функції, в тому числі константа, математичні та логічні вирази, виклик інших функцій, які повертають значення.

int main()
{
    int x, y;
    cin >> x >> y;
    int z = sum(x, y);             // виклик функції
    int k = sum(z, x + y);         // виклик функції
    int m = sum(k, sum(x + y, z)); // виклик функції
    int n = sum(3, 4);             // виклик функції
    cout << z << ' ' << k << ' ' << m << ' ' << n;
    return 0;
}

Аргументи (параметри), передані у функцію, є локальними для функції. Зміна значень аргументів всередині викликаної функції не впливає на значення в функції, з якої було здійснено виклик. Це відомо як передача за значенням і означає, що у функції створена локальна змінна, в якій зберігається значення кожного аргументу.

Аргументи, які передаються під час виклику функції, мають назву фактичних параметрів. Викликана функція має доступ до переданої інформації через так звані формальні параметри.

2.1.3 Тип результату void

Якщо функція не повертає ніяких значень, її тип повинен бути void.

void print(double a)
{
    cout << a << endl;
}

Тип void синтаксично є фундаментальним типом. Він може, однак, бути використаний тільки як частина складнішого типу; немає об'єктів типу void.

У тілі функції з типом результату void інструкція return може бути відсутня: тіло функції виконується до кінця програмного блоку. Якщо інструкція return присутня, то після її не повинно бути ні якого виразу. Інструкцію return можна використовувати для дострокового повернення з функції. Наприклад:

void printReciprocal(double a)
{
    if (a == 0)
    {
        return;
    }
    cout << 1 / a << endl;
}

Функцію з типом результату void можна викликати тільки окремою інструкцією (не всередині виразу).

int main()
{
    int x;
    cin >> x;
    printReciprocal(x); // виклик функції
    return 0;
}

2.1.4 Розташування функцій в програмі

Традиційна схема компіляції коду програми мовою C++ передбачає послідовну трансляцію тверджень без пошуку неоголошених імен нижче по тексту. Все, чим ми користуємось, повинно бути визначено або оголошено раніше. Це також стосується функцій. Для того, щоб можна було викликати функцію, її визначення (або прототип) повинно бути розташоване до виклику. В програмах, які використовують функції треба функцію, яку ми викликаємо, розташувати перед функцією, з якої здійснюється виклик:

#include <iostream>
using namespace std;

int sum(int a, int b)
{
    return a + b;
}

int main()
{
    int n = sum(3, 4);
    cout << n;
    return 0;
}

Альтернативний варіант – перед функцією main() розташувати прототип (або прототипи). Тоді функції, які ми викликаємо можна розташувати після функції main():

#include <iostream>
using namespace std;

int sum(int, int);

int main()
{
    int n = sum(3, 4);
    cout << n;
    return 0;
}

int sum(int a, int b)
{
    return a + b;
}

Прототипи можна повторювати багато разів, а також розташовувати всередині тіла функції:

#include <iostream>
using namespace std;

int main()
{
    int sum(int, int);
    int n = sum(3, 4);
    cout << n;
    return 0;
}

int sum(int a, int b)
{
    return a + b;
}

2.1.5 Локальні функції та лямбда-вирази

Функцію можна визначити всередині іншої функції. У C++ для визначення локальних функцій використовують альтернативний синтаксис – так звані лямбда-вирази, які з'явилися в C++ починаючи зі стандарту мови C++11. Лямбда-вираз (lambda expressions) – це вираз для представлення функцій всередині коду. Термін "лямбда" був узятий з математичної теорії рекурсивних функцій, де літера λ використовувалася для позначення функції. Синтаксис лямбда-виразу в C++ виглядає так:

[список захоплення] (список параметрів) { тіло функції }

У список захоплення можна включити імена локальних змінних або параметрів зовнішньої функції. Список захоплення (capture list) і список параметрів можуть бути порожніми. Нижче наведений приклад найпростішого лямбда-виразу:

[](){ cout << "Hello, world!" << endl; }

У найпростішому випадку лямбда-вираз може бути використано для виклику як звичайна функція:

[](){ cout << "Hello, world!" << endl; }();
cout << [](int a, int b) { return a * b; }(2, 2); // 4

Можна створити змінну, яка може бути використана для виклику:

auto f = [](int a, int b) { return a * b; };
cout << f(2, 2); // 4

Фактично створено локальну функцію з двома параметрами.

Тип результату визначається типом виразу після return. Якщо треба, тип результату можна вказати явно. Це можна зробити, помістивши операторі "стрілка" і тип між списком параметрів і тілом функції. У наведеному нижче прикладі результат перетворюється в тип int:

auto g = [](double a, double b) -> int { return a + b; };
cout << g(2.2, 2.3); // 4

Використання локальних функцій можна продемонструвати на прикладі обчислення відстані між двома точками на площині за такою формулою:

Стандартна бібліотека надає функцію обчислення квадратного кореня, але для обчислення другого степеня можна скористатися функцією pow(), що загалом неефективно, або множенням величини на себе, що не завжди зручно. Можна створити локальну функцію обчислення другого степеня. Програма буде такою:

#include <iostream>
using namespace std;

double distance(double x1, double y1, double x2, double y2)
{
    auto sq = [](double a) { return a * a; };
    return sqrt(sq(x2 - x1) + sq(y2 - y1));
}

int main()
{
    cout << distance(1, 1, 4, 5) << endl;
    return 0;
}

Наведений нижче приклад демонструє використання списку захоплення. Функція виводить значення параметрів, потім параметри замінюються зворотними величинами і ми хочемо тримати змінені параметри.

#include <iostream>
using namespace std;

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printParams();
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    printParams();
}

int main()
{
    printReciprocalValues(3, 4, 5);
}

Захоплення здійснюється один раз. Тому однакові значення будуть виведені двічі:

3 4 5
3 4 5

Для того, щоб вивести змінені значення, необхідно визначити іншу локальну функцію та здійснити нове захоплення. Код функції printReciprocalValues() тепер буде таким:

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printParams();
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    auto printModified = [a, b, c]() { cout << a << " " << b << " " << c << "\n"; };
    printModified();
}

Тепер результат буде іншим:

3 4 5
0.333333 0.25 0.2

Для того, щоб обійтися однією функцією, замість списку захоплення слід скористатися списком параметрів:

void printReciprocalValues(double a, double b, double c)
{
    auto printParams = [](double a, double b, double c) { cout << a << " " << b << " " << c << "\n"; };
    printParams(a, b, c);
    a = 1 / a;
    b = 1 / b;
    c = 1 / c;
    printParams(a, b, c);
}

Починаючи з C++11, синтаксис, аналогічний лямбда-виразам (без списку захоплення), можна використовувати для опису звичайних функцій. Наприклад, замість оголошення функції

int sum(int a, int b);

можна писати:

auto sum(int a, int b) -> int;

Відповідні заголовки можна використовувати під час реалізації функції.

auto sum(int a, int b) -> int
{
    return a + b;
}

З практичної точки зору такий синтаксис для звичайних (не локальних) функцій не надає переваг.

2.2 Область видимості

2.2.1 Загальні концепції

Кожен програмний об'єкт, зокрема змінна, має свою область видимості, яка визначає, де саме в програмі цей об'єкт може бути доступний.

Змінні можна створити всередині тіла функції, або іншого програмного блоку. Такі змінні є локальними змінними. Вони існують тільки всередині функції під час її виконання. Формальні параметри також є локальними змінними.

Глобальні змінні мають глобальну область видимості. Вони доступні в будь-якому місці програми. Глобальні змінні, визначені поза тілом функції, доступні з будь-якої функції в програмі, у тому числі з функції main(). Локальні змінні з тим же ім'ям, що й глобальні змінні, не пов'язані з відповідними глобальними змінними. Але локальна змінна з таким же ім'ям, як і глобальна змінна, приховує глобальну змінну. В таких випадках для доступу до глобальної змінної використовують операцію доступу до області видимості :: (scope resolution operator). Наприклад:

int k = 1;

void f()
{
    int k = 2;
    cout << k;   // 2
    cout << ::k; // 1
}

Синтаксис мови C++ дозволяє використовувати глобальні змінні, їх використання є небажаним. Глобальні змінні створюють небезпеку, оскільки вони є спільними даними. Будь-яка функція може змінити значення глобальної змінної, після чого інша функція, в якій передбачено використання певного значення глобальної змінної, може неправильно виконуватися. Такі помилки дуже важко знаходити.

Всередині блоку, який визначає тіло функції, можна створювати локальні блоки. В них можна створювати свої локальні змінні. У C++ можна у внутрішньому блоці визначати імена, вже описані в зовнішньому блоці:

{
    int i = 0;
    {
        int i = 2; // нова змінна
    }
}

Тепер до змінної i немає доступу з внутрішнього блоку. Немає синтаксичних конструкцій, які можуть забезпечити такий доступ. Подібні визначення призводять до виникнення неочевидних помилок. Слід уникати таких конструкцій.

2.2.2 Статичні локальні змінні

Як правило, локальні змінні, створені у функції, зникають після виходу з функції. Коли виклик функції здійснюється знову, зміні створюються та ініціалізуються заново. Якщо треба, щоб дані зберігалися протягом усього життєвого циклу програми, така змінна може бути визначена як статична (з модифікатором static). Ініціалізація виконується тільки тоді, коли функція викликається вперше, а змінні зберігають свої значення проміж викликами функції. Наведений нижче приклад демонструє відмінність між звичайними (автоматичними) і статичними локальними змінними:

#include <iostream>

using namespace std;

void localVariables()
{
    int m = 0;
    static int n = 0;
    m++;
    n++;
    cout << m << " " << n << endl;
}

int main()
{
    localVariables(); // 1 1
    localVariables(); // 1 2
    localVariables(); // 1 3
    return 0;
}

Не зважаючи на те, що статичні змінні існують протягом життєвого циклу програми, не існує механізмів доступу до таких змінних ззовні функції. Це зменшує ймовірність помилок.

2.3 Рекурсія

Функція може викликати себе. Такий механізм має назву рекурсії.

Рекурсія може бути безпосередньою або опосередкованою. Безпосередня рекурсія передбачає виклик функції безпосередньо з цієї функції:

void f() {
    ...
    f();
    ...
}

Важливо відзначити, що коли функція викликає саму себе, створюється нова копія даних цієї функції. Локальні змінні в новій копії не залежать від локальних змінних попередньої копії.

Неправильне вживання рекурсії може призвести до переповнення стека викликів.

Іноді рекурсія може бути використана замість циклу. Але слід пам'ятати, що в більшості задач рекурсія знижує ефективність через і створює труднощі зі зневадження.

Використання рекурсії доцільне в задачах обходу деревоподібних структур даних, зокрема, підкаталогів файлової системи.

Використовуючи рекурсію, можна обчислити суму

y = 12 + 22 + 32 + ... + n2

взагалі без циклів:

#include <iostream>

using namespace std;

double sum(int n)
{
    if (n <= 1)
    {
        return 1;
    }
    else
    {
        return n * n + sum(n - 1);
    }
}

int main()
{
    cout << sum(5);
    return 0;
}

Загалом такий підхід не є бажаним, погіршує розуміння коду та може призвести до помилок.

Опосередкована рекурсія передбачає, що перша функція викликає другу, а потім друга викликає першу функцію. В цьому випадку обов'язково необхідно створити прототип принаймні однієї з функцій:

void f(); // прототип
void g() {
    ...
    f();
    ...
}
void f() {
    ...
    g();
    ...
}

Опосередкована рекурсія може бути застосована для спрощення реалізації деяких алгоритмів. Наприклад, її можна використати для знаходження простих чисел:

#include <iostream>
using namespace std;

unsigned int nextPrime(unsigned int); // прототип

// Перевіряє, чи є число простим
bool isPrime(unsigned int number)
{
    unsigned int prime = 2; // перше просте число
    // Перевіряємо до кореня з number, чи ділиться number на якесь просте число:
    while (prime * prime <= number && number % prime != 0)
    {
        prime = nextPrime(prime);
    }
    return number % prime; // true якщо не ділиться
}

// Знаходить наступне просте число після number
unsigned int nextPrime(unsigned int number)
{
    unsigned int prime = number + 1;
    while (!isPrime(prime))
    {
        prime++;
    }
    return prime;
}

int main()
{
    setlocale(LC_ALL,"UKRAINIAN");
    unsigned int n;
    cout << "Уведіть ціле додатне число: ";
    cin >> n;
    cout << "Число " << n << (isPrime(n) ? " " : " не ") << "є простим.\n";
    cout << "Наступне після " << n << " просте число дорівнює " << nextPrime(n);
    return 0;
}

Цей алгоритм, звичайно, не є найбільш ефективним, але передбачає відносно прозору реалізацію.

2.4 Функції-підстановки

Коли здійснюється виклик функції, виконання програми переходить до відповідної групи інструкцій. Коли виконання функції завершується, виконання переходить назад на наступний рядок функції, з якої було здійснено виклик. Ці дії можуть бути пов'язані з деяким зниженням ефективності виконання.

Існують так звані функції-підстановки, або вбудовані. Такі функції мають модифікатор inline:

inline int min(int a, int b)
{
    return a < b ? a : b;
}

Якщо функція оголошена як вбудована, компілятор підставляє в точку виклику її тіло. Доцільно з модифікатором inline описувати найпростіші функції, багаторазове підставляння яких не істотно вплине на розміри програми.

Функція-підстановка не може бути рекурсивною. Якщо до заголовку такої функції додати модифікатор inline, він був проігнорований компілятором.

Сучасні компілятори намагаються конвертувати всі функції на функції-підстановки, якщо це можливо і підвищує продуктивність програми. Проте явне використання модифікатора inline дозволяє визначити функцію декілька разів, що важливо з точки зору розташування таких визначень у заголовних файлах.

2.5 Перевантаження імен функцій

Мова C++ дозволяє створити декілька функцій з однаковими іменами. Це називається перевантаженням імен функцій (function name overloading). Перевантажені функції дозволяють програмістам реалізувати різну семантику для функції, залежно від типів і кількості аргументів.

Функції повинні відрізнятися списками параметрів: різними типами параметрів, різним числом параметрів, або обома ознаками. Наприклад:

int sum(int a, int b)
{
    return a + b;
}

double sum(double a, double b)
{
    return a + b;
}

double sum(double a, double b, double c)
{
    return a + b + c;
}

int main()
{
    cout << sum(1, 2) << endl;      // перша функція sum()
    cout << sum(1.0, 2.5) << endl;  // друга функція sum()
    cout << sum(1, 2, 2.6) << endl; // третя функція sum()
    return 0;
}

Примітка: дві функції з однаковим ім'ям і списком параметрів, але з різними типами результату, генерують помилку компіляції:

int f(double x);
double f(double x); // Помилка!

2.6 Усталені значення аргументів

У багатьох випадках для аргументів функції можна вказати усталені значення (default values), які можуть бути цілком задовільними в багатьох випадках. Для розв'язання цієї проблеми реалізовано механізм аргументів з усталеними значеннями, що дозволяє визначати лише ті аргументи функції, які є істотними в конкретному контексті. Наприклад:

int sum(int x, int y = 0, int z = 0)
{
    return x + y + z;
}

int main()
{
    cout << sum(5) << endl;       // 5, y = 0, z = 0
    cout << sum(1, 2) << endl;    // 3, z = 0
    cout << sum(1, 2, 5) << endl; // 8
    return 0;
}

Аргументи з усталеними значеннями використовують у випадках, коли параметри в кінці списку можуть бути відсутні. Усі параметри функції можуть бути з усталеними значеннями. Слід пам'ятати, що аргументи з усталеними значеннями повинні бути останніми в списку:

void f(double x, int y = 0, int h); // помилка

Усталене значення не може бути повторене в більш пізніх описах функції, навіть якщо перевизначення ідентичне оригіналу. Таким чином, наведений нижче код видає помилку:

void f(double x, int y = 1);
void f(double x, int y = 1) { } // помилка 
  // Слід писати void f(double x, int y) { }

2.7 Посилання

2.7.1 Загальні концепції

У мові C++ визначено механізм створення так званих посилань. Посилання (reference) може бути визначене як друге ім'я (псевдонім) існуючої змінної (об'єкта).

Можна описати посилання зазначенням типу, за яким слідує оператор посилання (&) та ім'я посилання:

int i = 10; 
int &j = i; // посилання на i
j = 11;
cout << i;  // 11

Не можна створювати посилання, не вказуючи об'єкт, на який ми посилаємось. Посилання повинні бути ініціалізовані під час створення:

int &k; // синтаксична помилка!

Можна визначити посилання на константний об'єкт:

int m = 2; 
const int &n = m; // посилання на m
double x = n + 1; // OK
m = 11;           // OK
n = 12;           // помилка!

2.7.2 Посилання як аргументи функції

Посилання можуть бути використані як аргументи функції. Припустимо, необхідно створити функцію, яка обмінює значення двох цілих змінних. Перша версія функції буде такою:

void swap(int x, int y)
{
    int z = x;
    x = y;
    y = z;
}

Можна спробувати викликати цю функцію, але на жаль значення змінних a і b залишились такими, якими вони були раніше, тоді як значення x і y у функції swap() змінились (можна перевірити за допомогою зневаджувача):

void swap(int x, int y) // x = 1, y = 2
{
    int z = x;
    x = y;
    y = z; // x = 2, y = 1
}

int main()
{
    int a = 1;
    int b = 2;
    swap(a, b);
    cout << a << endl; // 1
    cout << b << endl; // 2
    return 0;
}

Проблема пов'язана з тим, що змінені значення праметрів не копіюються назад у функцію main().

Використання посилань допоможе ров'язати цю проблему. Якщо описати параметри як посилання, під час виклику створюються синоніми змінних, які надіслані як фактичні параметри:

void swap(int &x, int &y)
{
    int z = x;
    x = y;
    y = z;
}

Фактично у функції ми працюємо з тими ж змінними, яки ми створили у функції main():

int main()
{
    int a = 1;
    int b = 2;
    swap(a, b);
    cout << a << endl; // 2
    cout << b << endl; // 1
    return 0;
}

Параметри-посилання можна також використовувати для того, щоб повернути з функції декілька результатів. Наприклад, необхідно розв'язати таке рівняння:

|x| – b = 0

Оскільки коренів – два, доцільно використати параметри-посилання:

#include <iostream>
using namespace std;

void solveEquation(double b, double& x1, double& x2)
{
    x1 = b;
    x2 = -b;
}

int main()
{
    double b, x1, x2;
    cin >> b;
    solveEquation(b, x1, x2);
    cout << "x1 = " << x1 << " x2 = " << x2;
    return 0;
}

2.7.3 Використання посилань на константний об'єкт

Передача параметрів за посиланням може також бути використана для передачі у функцію великих об'єктів (структури й класи будуть розглянуті пізніше). Замість того, щоб копіювати об'єкт через стек викликів, достатньо передати його адресу, як це здійснюється для посилань. Але при цьому виникає небезпека випадкової зміни значення об'єкта, оскільки у функції ми продовжуємо працювати з тим самим об'єктом, що і в місці виклику. Крім того, не можна надсилати константи як параметри. В таких випадках можна скористатися посиланням на константний об'єкт. Змінювати значення такого параметра в тілі функції неможливо.

Наприклад, нам треба знайти третій степінь числа типу double. Ми передаємо число через посилання з модифікатором const. Всередині тіла функції змінити значення такого параметра заборонено:

double cube(const double &x)
{
    double y = x * x * x;
    x = 3; // помилка!
    return y;
}

Виправивши помилку, ми можемо використовувати цю функцію, в тому числі для параметрів-констант та виразів, бо константи теж розташовані в пам'яті та мають адресу:

#include <iostream>
using namespace std;

double cube(const double &x)
{
    double y = x * x * x;
    return y;
}

int main()
{
    double x = 4;
    const double c = 3;
    cout << cube(x) << endl;
    cout << cube(c) << endl;
    cout << cube(1.6) << endl;
    cout << cube(6 - 4) << endl;
    return 0;
}

2.7.4 Посилання як результат функції

Посилання можуть бути використані як тип результату функції. Дуже важливо бути впевненим, що посилання пов'язане зі змінною, яка існує після виходу з функції:

int& f()
{
    int k;
    return k; // Помилка: k знищується після виходу з функції
}

А це правильно:

int& f()
{
    static int k;
    return k; // OK
}

int main()
{
    f() = 10;
    cout << f(); // 10
    return 0;
}

Функція повертає псевдонім статичної змінної, яка не знищується після виходу з функції. Таким чином, ми можемо здійснити таке присвоєння:

f() = 10; // k = 10

Ми присвоюємо значення не функції, а її результату – змінній, посилання на яку функція повертає.

Функцію, яка повертає посилання, можна використати, наприклад, для того, щоб до групи змінних можна було б звертатися в циклі:

#include <iostream>
using namespace std;

double x, y, z;

double& variable(int k)
{
    switch (k)
    {
        case 1:  return x;
        case 2:  return y;
        default: return z;
    }
}

int main()
{
    for (int i = 1; i <= 3; i++)
    {
        variable(i) = i;
    }
    cout << x << " " << y << " " << z; // 1 2 3
    return 0;
}

Важливо, щоб функція завжди повертала посилання на яку-небудь змінну, тому посилання на z доцільно повертати для будь-якого значення, а не тільки для 3.

2.8 Структура програми, яка використовує функції

Найпростіше застосування функцій в програмі – виділити окремі частини, пов'язані з конкретними алгоритмами обробки інформації. Такі частини повинні мати фіксований набір вихідних даних, фіксований набір результатів, а також бути незалежними від коду інших функцій. Для здійснення інформаційного обміну в коді функцій можна використовувати глобальні змінні, але слід мінімізувати використання таких змінних.

Майже всі програми можна розділити на відносно незалежні частини. Для такої структуризації програми можна також застосувати окремі функції та послідовно викликати їх з функції main().

Програма, яка обчислює деякі значення, як правило, містить частини, відповідальні за введення, розрахунки і виведення.

Припустимо, що нам необхідно реалізувати програму, яка обчислює суму квадратів цілих чисел:

y = 12 + 22 + 32 + ... + n2

Перша реалізація не поділена на частини:

#include <iostream>
using namespace std;

int main()
{
    int n;
    cout << "Input n:";
    cin >> n;
    int y = 0;
    for (int i = 1; i <= n; i++)
    {
        y += i * i;
    }
    cout << "y = " << y;
    return 0;
}

Найпростіше рішення полягає у використанні глобальних змінних:

#include <iostream>
using namespace std;

int n;
int y = 0;

void read()
{
    cout << "Input n:";
    cin >> n;
}

void calc()
{
    for (int i = 1; i <= n; i++)
    {
        y += i * i;
    }
}

void write()
{
    cout << "y = " << y;
}

int main()
{
    read();
    calc();
    write();
    return 0;
}

Використання глобальних змінних не є гарною ідеєю. Кращий підхід полягає у використанні параметрів:

#include <iostream>
using namespace std;

int read()
{
    int n;
    cout << "Input n:";
    cin >> n;
    return n;
}

int calc(int n)
{
    int y = 0;
    for (int i = 1; i <= n; i++)
    {
       y += i * i;
    }
    return y;
}

void write(int y)
{
    cout << "y = " << y;
}

int main()
{
    int n = read();
    int y = calc(n);
    write(y);
    return 0;
}

Функція main() може бути реалізована взагалі без змінних:

...

int main()
{
    write(calc(read()));
    return 0;
}

Функції, на які ми розділили велику програму, повинні бути не дуже довгими, наприклад, до 20 рядків коду, в іншому випадку її краще розділити на декілька функцій.

Важливо, щоб функція, яка призначена для отримання результату, не здійснювала одночасно виведення цього результату на консоль, якщо це не обумовлене завданням. Припустимо, наприклад, що нам треба створити функцію, яка обчислює третій степінь числа, а потім вивести результат. Замість об'єднання в одній функції обчислення й виведення

double cube(double x)
{
    double y = x * x * x;
    cout << y;
    return y;
}

краще здійснити виведення у функції main(), або створити окрему функцію для виведення:

double cube(double x)
{
    return y = x * x * x;
}

void printCube(double x)
{
    cout << cube(x);
}

Функція, яка лише повертає результат, а не виводить його на консоль, може бути більш універсальною: її можна викликати багато разів у виразах, а також використовувати не тільки в консольних застосунках. Це також стосується введення даних. Необхідні дані краще передавати як параметри.

2.9 Використання стандартних функцій

Перед тим, як реалізовувати алгоритми обробки даних, зокрема, створювати власні функції, доцільно переконатися, що ці алгоритми не реалізовані стандартними функціями.

Для того, щоб скористатися стандартною функцією в програмі, необхідно підключити заголовний файл, в якому знаходиться оголошення (прототип) відповідної функції. Заголовні файли з відповідними функціями розташовані в теці include і постачаються разом з компілятором, лінкером та іншими засобами для створення програм мовою C++. Реалізація функцій у скомпільованому вигляді знаходиться у файлах з розширенням .lib. Якщо середовище програмування було коректно встановлене, немає потреби відшукувати ці файли. Компілятор і лінкер обізнані про їхнє розташування.

Окрім оголошень функцій у заголовних файлах розташовані необхідні типи і константи.

У заголовному файлі cmath знаходяться оголошення математичних функцій. У таблиці наведені найбільш вживані математичні функції:

Функція Зміст Приклад виклику
double pow(double a, double b) Обчислення ab pow(x, y)
double sqrt(double a) Обчислення квадратного кореня sqrt(x)
double sin(double a) Обчислення синуса sin(x)
double cos(double a) Обчислення косинуса cos(x)
double tan(double a) Обчислення тангенса tan(x)
double asin(double a) Обчислення арксинуса asin(x)
double acos(double a) Обчислення арккосинуса acos(x)
double atan(double a) Обчислення арктангенса atan(x)
double exp(double a) Обчислення ex exp(x)
double log(double a) Обчислення натурального логарифма log(x)
int abs(int a)
double abs(double a)
 Знаходження модуля числа abs(x)
double fabs(double a)
 Знаходження модуля числа fabs(x)
long round(double a) Округлення до найближчого цілого round(x)

Для тригонометричних функцій аргумент вказується в радіанах.

У наведеному нижче прикладі здійснюється демонстрація роботи математичних функцій:

#include <iostream>
using namespace std;

int main()
{
    double x = 2;
    cout << pow(x, 4) << endl; // 16
    cout << sqrt(x)   << endl; // 1.41421
    cout << sin(x)    << endl; // 0.909297
    cout << cos(x)    << endl; // -0.416147
    cout << tan(x)    << endl; // -2.18504
    cout << asin(x)   << endl; // -nan(ind), математична помилка
    cout << atan(x)   << endl; // 1.10715
    cout << exp(x)    << endl; // 7.38906
    cout << log(x)    << endl; // 0.693147
    x = -2.8;
    cout << abs(x)    << endl; // 2.8
    cout << round(x)  << endl; // -3
    return 0;
}

Заголовний файл ctime дозволяє працювати з часом та датами. Функція time() повертає час у секундах, що минув з півночі 1 січня 1970 року, або -1, якщо є помилка.

Наприклад, в такий спосіб можна отримати поточний час:

long long currentTime = time(NULL);

В попередніх прикладах для використання літер української абетки здійснювався виклик функції setlocale(), оголошеної в заголовному файлі clocale:

setlocale(LC_ALL, "UKRAINIAN");

Стандартні заголовні файли часто містять включення інших файлів. Наприклад, заголовний файл iostream підключає clocale.

Прототипи деяких найбільш універсальних функцій можна знайти у заголовному файлі cstdlib. Наприклад, для здійснення тестування програм, пов'язаних з обчисленнями, дуже часто треба користуватися так званими випадковими числами. Значення випадкового числа заздалегідь не можна передбачити, але можна оцінити ймовірність значення, або отримання числа з певного діапазону. Найпростіший випадок – так звані рівномірно розподілені числа: ймовірність виникнення кожного окремого значення в межах діапазону однакова. Найчастіше працюють з випадковими значеннями цілого типу. Якщо достатньо довго отримувати такі числа, кожне значення з вибраного діапазону з'явиться приблизно однакову кількість разів.

Для отримання випадкових цілих чисел використовують функцію rand():

int rand();

Функція rand() повертає ціле значення, яке лежить в межах від 0 до 32767 включно. Якщо нам треба отримати числа з меншого діапазону, доцільно скористатись операцією отримання залишку від ділення. Наприклад, програма генерує числа в діапазоні від 0 до 9 включно:

#include <cstdlib>
#include <iostream>

using namespace std;

int main()
{
    for (int i = 0; i < 100; i++)
    {
        int k = rand() % 10;
        cout << k << " ";
    }
    return 0;
}

Функція rand() генерує так звані псевдовипадкові числа. Хоч вони і рівномірно розподілені по вказаному діапазону, послідовність чисел повторюється під час кожного запуску програми. Ми отримуємо так звані псевдовипадкові числа. Генерування таких чисел здійснюється, починаючи з певного початкового цілого значення. Це число можна визначати за допомогою функції srand() параметром цілого типу. Визначаючи кожного разу різні значення, можна отримати різні послідовності псевдовипадкових чисел.

Для того, щоб отримати справжні випадкові числа, генератор слід ініціалізувати дійсно випадковим числом. Кількість секунд, яку повертає функція time(), звичайно кожного разу буде іншою, тому послідовність чисел кожного разу буде новою і тепер числа будуть насправді випадковими. Наша попередня програма, яка генеруватиме випадкові числа, буде такою:

#include <cstdlib>
#include <ctime>
#include <iostream>

using namespace std;

int main()
{
    srand(time(NULL));
    for (int i = 0; i < 100; i++)
    {
        int k = rand() % 10;
        cout << k << " ";
    }
    return 0;
}

Заголовний файл cstdlib також містить оголошення функції system(). Параметр цієї функції – рядок, який містить певну команду операційної системи. Це може бути вбудована команда ядра операційної системи, стандартна утиліта, або навіть програма, створена раніше користувачем.

Наприклад, працюючи під орудою операційної системи Windows, так можна очистити консольне вікно:

system("cls");

Можна забезпечити затримку роботи програми до натиснення будь-якої клавиші:

system("pause");

Можна запустити будь-яку програму, наприклад, блокнот:

system("notepad");

Можна також встановити необхідну сторінку кодової таблиці для роботи консольного застосунку. Наприклад, так можна встановити кириличну сторінку кодової таблиці:

system("chcp 1251");

Після встановлення сторінки у консольному вікні з'являється повідомлення "Active code page: 1251". Щоб придушити появу цього повідомлення, його можна переадресувати в файл, або в умовний об'єкт з ім'ям nul (ніщо):

system("chcp 1251 > nul");

Заголовний файл cstring надає прототипи функцій для роботи з рядками, які закінчуються нулевим символом (null-terminated strings). У заголовному файлі cstdio містяться оголошення функцій, які реалізують введення та виведення в стилі мови C (наприклад, scanf(), printf() тощо). Більш детально функції цих заголовних файлів будуть розглянуті пізніше.

Всі функції стандартної бібліотеки визначені в просторі імен std.

3 Приклади програм

3.1 Сума послідовних степенів числа

У наведеній нижче програмі вводиться величина x і ціле значення n. Необхідно обчислити суму послідовних цілих степенів x від 1 до n.

#include <iostream>

using namespace std;

double sumOfPowers(double x, int n)
{
    double sum = 0;
    double power = 1;
    // Степені та суму можна розрахувати за один цикл:
    for (int i = 0; i < n; i++)
    {
        power *= x;
        sum += power;
    }
    return sum;
}

int main()
{
    double x;
    int n;
    cout << "Enter x and n:";
    cin >> x >> n;
    cout << sumOfPowers(x, n);
    return 0;
}

3.2 Статичні локальні змінні

У наведеній нижче програмі обчислюється сума цілих значень які вводить користувач:

#include <iostream>
  
using namespace std;

int add(int i)
{
    static int sum = 0;
    sum += i;
    return sum;
}

int main()
{
    int i;
    do
    {
        cin >> i;
        cout << add(i) << endl;
    }
    while (i);
    return 0;
}

3.3 Лінійне рівняння

Функція solve() в наведеному нижче прикладі знаходить корінь лінійного рівняння (аргумент, який передається за посиланням) i повертає кількість коренів. Якщо коренів безмежна кількість, функція повертає -1. Всередині функції main() доцільно створити перемикач, який аналізує кількість розв'язків і здійснює відповідні виведення.

#include <iostream>

using namespace std;

int solve(double a, double b, double& x)
{
    if (a == 0)
    {
        if (b == 0)
        {
            return -1;
        }
        else
        {
            return 0;
        }
    }
    x = -b / a;
    return 1;
}

int main()
{
    system("chcp 1251 > nul");
    double a, b, x;
    cin >> a >> b;
    int count = solve(a, b, x);
    switch (count)
    {
    case -1:
        cout << "Безмежна кількість розв'язкiв";
        break;
    case 0:
        cout << "Немає розв'язкiв";
        break;
    case 1:
        cout << "x = " << x;
    }
    cout << endl;
    return 0;
}

3.4 Таблиця значень функції

Припустимо, необхідно створити програму, яка на заданому діапазоні з певним кроком обчислює значення функції

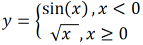
Окремі частини програми доцільно реалізувати як незалежні функції. Програма може бути такою:

#include <iostream>
#include <cmath>
using namespace std;

// функція введення даних з клавіатури, параметри передаються за посиланням
bool readData(double& from, double& to, double& step)
{
    cout << "Введiть початок, кінець інтервалу та крок: ";
    cin >> from >> to >> step;
    if (from >= to || step <= 0)
    {
        cerr << "Хибні дані" << endl;
        return false;
    }
    return true;
}

// Функція, визначена в завданні
double y(double x)
{
    if (x < 0)
    {
        return sin(x);
    }
    else
    {
        return sqrt(x);
    }
}

// Виведення значень аргументів і функції на інтервалі з визначеним кроком
void printInALoop(double from, double to, double step)
{
    cout << "x\ty" << endl; // "шапка" таблиці
    for (double x = from; x <= to; x += step)
    {
        cout << x << "\t" << y(x) << endl;
    }
}

int main()
{
    system("chcp 1251 > nul");
    double from, to, step;
    if (readData(from, to, step))
    {
        printInALoop(from, to, step);
        return 0; // таблицю виведено
    }
    return -1; // помилка введення даних
}

Розташування функцій у програмі визначається механізмом виклику. Функція, яка викликається, повинна передувати функції, яка її викликає. Такий порядок не завжди зручний з точки зору сприйняття коду людиною. Якщо спочатку розташувати прототипи функцій, порядок можна змінити:

#include <iostream>
#include <cmath>
using namespace std;

// Прототипи функцій:
bool readData(double &, double &, double &);
void printInALoop(double, double, double);
double y(double);

int main()
{
    system("chcp 1251 > nul");
    double from, to, step;
    if (readData(from, to, step))
    {
        printInALoop(from, to, step);
        return 0; // таблицю виведено
    }
    return -1; // помилка введення даних
}

// функція введення даних з клавіатури, параметри передаються за посиланням
bool readData(double& from, double& to, double& step)
{
    cout << "Введiть початок, кінець інтервалу та крок: ";
    cin >> from >> to >> step;
    if (from >= to || step <= 0)
    {
        cerr << "Хибні дані" << endl;
        return false;
    }
    return true;
}

// Виведення значень аргументів і функції на інтервалі з визначеним кроком
void printInALoop(double from, double to, double step)
{
    cout << "x\ty" << endl; // "шапка" таблиці
    for (double x = from; x <= to; x += step)
    {
        cout << x << "\t" << y(x) << endl;
    }
}

// Функція, визначена в завданні
double y(double x)
{
    if (x < 0)
    {
        return sin(x);
    }
    else
    {
        return sqrt(x);
    }
}

3.5 Створення функцій для роботи зі станом програми

В наведеному нижче прикладі відслідковується та змінюється стан програми. Значення констант (прапорів) – послідовні степені 2, функції setFlag(), removeFlag() та clearState() змінюють стан програми (глобальна змінна state). Функція printBinary() виводіть значення в двійковому вигляді . Програма демонструє зміну та аналіз стану:

#include <iostream>

using std::cout;

const unsigned char NO_DATA = 0;
const unsigned char DATA_READ = 1;
const unsigned char SOLVED = 2;
const unsigned char ROOTS_FOUND = 4;

unsigned char state = 0;

void setFlag(unsigned char flag)
{
    state |= flag;
}

void removeFlag(unsigned char flag)
{
    state &= ~flag;
}

bool checkState(unsigned char flag)
{
    return state & flag;
}

void clearState()
{
    state = NO_DATA;
}

void printBinary(unsigned char flag)
{
    const int size = sizeof(flag) * 8;
    for (int i = 0; i < size; i++)
    {
        cout << (flag >> (size - 1));
        flag <<= 1;
    }
    cout << "\n";
}

int main()
{
    system("chcp 1251 > nul");
    cout << "Прапори:\n";
    printBinary(NO_DATA);
    printBinary(DATA_READ);
    printBinary(SOLVED);
    printBinary(ROOTS_FOUND);

    cout << "Початковий стан\n";
    printBinary(state);

    cout << "Ввели данi\n";
    setFlag(DATA_READ);
    printBinary(state);

    cout << "Очистили данi\n";
    removeFlag(DATA_READ);
    printBinary(state);

    cout << "Знову ввели данi\n";
    setFlag(DATA_READ);
    printBinary(state);

    if (checkState(DATA_READ)) {
        std::cout << "Розв'язали рiвняння\n";
        setFlag(SOLVED);
        printBinary(state);
        setFlag(ROOTS_FOUND);
        printBinary(state);
    }
    std::cout << "Починаємо спочатку\n";
    clearState();
    printBinary(state);
    return 0;
}

Результати роботи програми будуть такими:

Прапори:
00000000
00000001
00000010
00000100
Початковий стан
00000000
Ввели данi
00000001
Очистили данi
00000000
Знову ввели данi
00000001
Розв'язали рiвняння
00000011
00000111
Починаємо спочатку
00000000

4 Вправи для контролю

  1. Створити програму для тестування функції signum().
  2. Здійснити розробку та тестування функції, яка обчислює добуток трьох аргументів.
  3. Здійснити розробку та тестування функції, яка обчислює добуток перших n непарних значень.
  4. Здійснити розробку та тестування функції, яка обчислює ex через суму.
  5. Здійснити розробку та тестування рекурсивної функції, яка обчислює факторіал.
  6. Здійснити розробку та тестування функції, яка здійснює виведення всіх парних значень в заданому діапазоні.
  7. Здійснити розробку та тестування функції, яка здійснює виведення добутку перших n парних значень.
  8. Здійснити розробку та тестування функції, яка обчислює найбільший спільний дільник двох цілих чисел.

5 Контрольні запитання

  1. Що таке функція?
  2. Що таке заголовок функції?
  3. Що таке тіло функції?
  4. Що таке прототип функції?
  5. Як створити локальну функцію?
  6. Що таке список захоплення?
  7. Як здійснюється передача параметрів у функцію?
  8. У чому різниця між формальними і фактичними параметрами?
  9. Чи є інструкція return завжди обов'язковою?
  10. Чи може функція з типом результату void містити твердження return?
  11. Що таке локальна змінна?
  12. Що таке область видимості (scope)?
  13. Що таке глобальна область видимості?
  14. Як отримати доступ до імен з глобальної області видимості?
  15. Чи можуть локальні змінні приховати глобальні змінні?
  16. У чому різниця між статичними і нестатичними локальними змінними?
  17. Яким є життєвий цикл статичної локальної змінної?
  18. Як використовують статичні локальні змінні?
  19. Що таке рекурсія?
  20. Що таке функція-підстановка (inline)?
  21. Як перевантажити ім'я функції?
  22. Чи можна створити дві глобальні функції з однаковими іменами і списками параметрів, але з різними типами результату?
  23. Як описати аргументи з усталеними значеннями?
  24. Що таке посилання?
  25. Як ініціалізувати посилання?
  26. Для чого використовують посилання?
  27. Для чого використовують посилання на константний об'єкт?
  28. Чи можна повернути посилання з функції?
  29. Які є варіанти обміну даними між різними функціями однієї програми?
  30. Що таке випадкове і псевдовипадкове число? Як отримати випадкові числа?

 

Попередня Наступна
up