1 Problem Statement
Assume that we need to develop a graphical user interface (GUI) application, which finds roots of a quadratic equation whose coefficients are functions of the parameter t.
f(t) · x2 + g(t) · x + c = 0
The functions f(t) and g(t) can be arbitrary. In our example, they will be defined as follows:
f(t) = (a0 + a1) (a1 + a2) ... (am – 1 + am) – t
g(t) = x0 y0 + x1 y1 + ...+ xn yn + t
The program should provide the following functions
- keyboard data input
- reading data from XML-file
- editing source data
- storing data in another XML-file
- calculating roots
- graphical interpretation,
- generation and storing report,
- providing help information.
2 Requirements Setting. Analysis and Design
2.1 Use Case Diagram
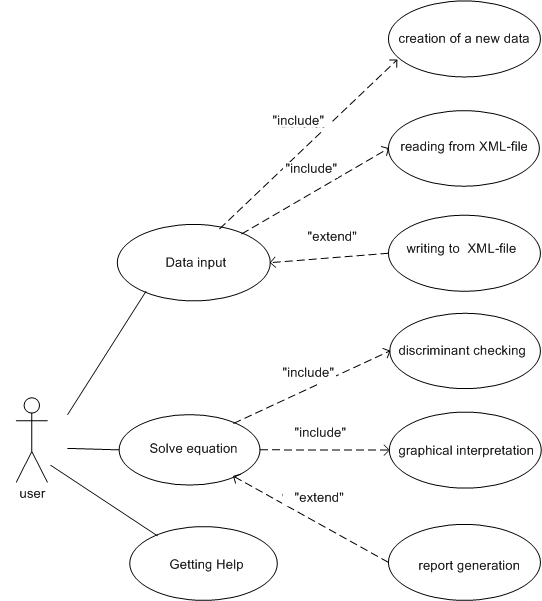
Program requirements are represented on use case diagram.
This diagram should include one actor (user), who can interact with our program in several ways:
- creation of a new blank project for data input
- reading data from an XML file
- writing modified data to another XML file
- solving equation with graphical interpretation; solving should include discriminant checking
- report generation
- getting help.
Figure 2.1 shows use case diagram
.
2.2 Development of Data Structure and Test Preparation
Before program development we should prepare source data. According to problem setting data should be represented in the form of XML document. In our case, equation is defined by a set of numbers ai and bj, and c value. The following schema file can be proposed:
<?xml version="1.0" encoding="utf-8"?> <xs:schema xmlns:xs="http://www.w3.org/2001/XMLSchema"> <xs:element name="EquationData"> <xs:complexType> <xs:sequence> <xs:element name="ACoefs"> <xs:complexType> <xs:sequence> <xs:element maxOccurs="unbounded" name="ACoef"> <xs:complexType> <xs:attribute name="Value" type="xs:double" use="required" /> <xs:attribute name="Index" type="xs:int" use="required" /> </xs:complexType> </xs:element> </xs:sequence> </xs:complexType> </xs:element> <xs:element name="XYCoefs"> <xs:complexType> <xs:sequence> <xs:element maxOccurs="unbounded" name="XYCoef"> <xs:complexType> <xs:attribute name="X" type="xs:double" use="required" /> <xs:attribute name="Y" type="xs:double" use="required" /> </xs:complexType> </xs:element> </xs:sequence> </xs:complexType> </xs:element> </xs:sequence> <xs:attribute name="CCoef" type="xs:double" use="required" /> </xs:complexType> </xs:element> </xs:schema>
Note: the indices for the coefficients are significant; however, we cannot rely on the order in which elements are located in an XML document (the order can be arbitrary), so indexes should be stored separately.
Here is an example of XML document that describes an equation.
<?xml version="1.0"?> <EquationData CCoef="-2"> <ACoefs> <ACoef Value = "3" Index="0" /> <ACoef Value = "1" Index="1" /> <ACoef Value = "0" Index="2" /> <ACoef Value = "0.25" Index="3" /> </ACoefs> <XYCoefs> <XYCoef X = "-1" Y = "2" /> <XYCoef X = "1" Y = "1" /> <XYCoef X = "0.0" Y = "0.1" /> </XYCoefs> </EquationData>
We can save this data, for example, in the EquationCommon.xml file (it describes the general case). Several file variants should be prepared for software testing. For example, if we change the value of CCoef (-2) to any positive, for example, 2, the equation will have no solutions. We can save this option in the EquationNoSolutions.xml file. We can also create files in which the coefficient at the second power of x will be 0. This is LinearEquation.xml:
<?xml version="1.0"?>
<EquationData CCoef="6">
<ACoefs>
<ACoef Value = "1" Index="0" />
<ACoef Value = "1" Index="1" />
<ACoef Value = "0" Index="2" />
<ACoef Value = "0" Index="3" />
</ACoefs>
<XYCoefs>
<XYCoef X = "-1" Y = "2" />
<XYCoef X = "1" Y = "1" />
<XYCoef X = "0" Y = "1" />
</XYCoefs>
</EquationData>
As well as LinearEquationNoSolutions.xml:
<?xml version="1.0"?>
<EquationData CCoef="6">
<ACoefs>
<ACoef Value = "1" Index="0" />
<ACoef Value = "1" Index="1" />
<ACoef Value = "0" Index="2" />
<ACoef Value = "0" Index="3" />
</ACoefs>
<XYCoefs>
<XYCoef X = "-1" Y = "0" />
<XYCoef X = "0" Y = "1" />
<XYCoef X = "0" Y = "1" />
</XYCoefs>
</EquationData>
2.3 Definition of a Class Structure
The class diagram from a conceptual point of view can be as follows:
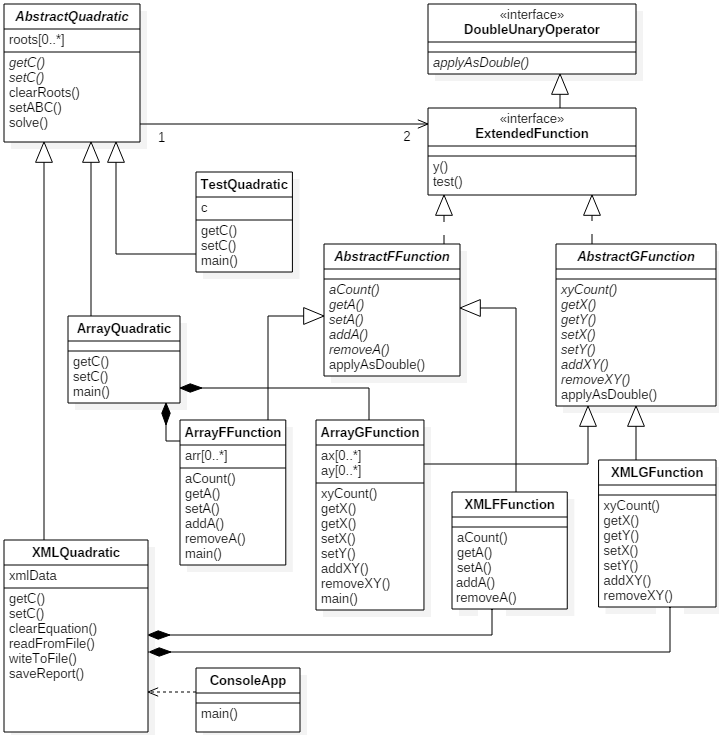
The main entity of the domain is the AbstractQuadratic class that represents quadratic equation. This class allows us to solve equations in general. The class is abstract because it does not define the mechanism of storage of the coefficient c. We can implement the function of data cleansing (clearRoots()), the function of determining the coefficients, solving the equation (solve()) depending on the value of the parameter t, The coefficients a and b can be represented as a reference to an object that implements a specific functional interface. We can also extend an existing functional interface, such as java.util.function.DoubleUnaryOperator, by adding test() method with the default implementation that calculates and outputs function values at a specified interval with a specific step. For convenience, we can also define y() function that can be called instead of applyAsDouble().
The TestQuadratic class performs the simplest implementation of the functions f and g to test different cases of solving the equation.
The classes that implement the ExtendedFunction interface, AbstractFFunction and AbstractGFunction, provide the appropriate implementation of the applyAsDouble() method according to the formulas defined in the problem statement. To obtain the necessary data (coefficients a and pairs of values x and y) we declare abstract methods, the implementation of which will depend on the particular data storage mechanism (array, vector, list, etc.) and will be defined in derived classes. In particular, the ArrayFFunction and ArrayGFunction classes implement the corresponding methods by accessing arrays, and the XMLFFunction and XMLGFunction classes use data stored in XML documents and are read using means of JAXB.
Classes derived from AbstractQuadratic, ArrayQuadratic, and XMLQuadratic use ArrayFFunction / ArrayGFunction and XMLFFunction / XMLGFunction class pairs, respectively, to represent functions.
The ConsoleApp class demonstrates and tests software classes.
Later, classes that implement the graphical user interface will be added to the class diagram, as well as refinements will be made, in particular, exception classes and other auxiliary classes will be added.
3 Creation of Essential Classes. Implementation of Console Test
3.1 Creating a New JavaFX Project and Defining its Structure
We create a new Java project called ParametrizedQuadratic. in the IntelliJ IDEA programming environment. For successful application of JAXB technology, JDK 1.8 should be used for the project. We also create the ua.inf.iwanoff.quadratic package.
Note. Files and options required to work with JavaFX classes can be added manually.
In order to minimize the probability of creating masonry from classes, it is advisable to create a separate model package. The model package should contain classes that describe our domain and data processing algorithms.
3.2 Creating Abstract Classes and Classes for Testing
The development of classes should start with the extension of the existing functional interface java.util.function.DoubleUnaryOperator which declares the method applyAsDouble() with a parameter and result of type double. The new ExtendedFunction interface will look like this:
package ua.inf.iwanoff.quadratic.model;
import java.util.function.DoubleUnaryOperator;
public interface ExtendedFunction extends DoubleUnaryOperator {
default double y(double x) {
return applyAsDouble(x);
}
default String test(String argName, String funcName, double from, double to, double step) {
StringBuilder sb = new StringBuilder("");
for (double x = from; x <= to; x += step) {
sb.append(String.format(argName + " = %9.4f " +
funcName + "(" + argName + ") = %9.4f%n", x, y(x)));
}
return sb.toString();
}
}
The created interface is also functional, as it has only one abstract function: the added methods have default implementation. This will allow us to define the required functions both through the classes that implement this interface and through lambda expressions and method references.
We can now implement the AbstractQuadratic class, which will contain a definition of the references to the functions f and g, as well as a list of roots. The class can fully implement the logic of solving the equation. Only access to the coefficient c is represented by the abstract functions getC() and setC(). The clearRoots() function resets the object (when the equation has not been solved). This function should be called from all setters, as well as from the setABC() function, which allows us to define all the source data.
The main method that allows us to solve the equation is the solve() method. The quadratic equation is solved for a certain value of the parameter t. If there are no roots, the list of roots will be 0. If the equation is solved, the length of the list will be 1 for the linear equation and 2 for the quadratic equation. To denote the infinite count of roots, an item with a value of null is added to the list. The getRoots() method returns a copy of the root list.
Note: it is important to return the copies of the elements, not the reference to the list, as this will prevent incorrect modification of the list of roots.
It is advisable to return modified object (this) from the methods that alter the state of an object (setC(), clearRoots(), setF(), setG(), setABC(), and solve()) . This will create a chain of method calls.
We can override the toString() method to properly display the results of solving the equation. The results are displayed depending on the contents of the list of roots and their number.
In the main() function, we create a local class derived from AbstractQuadratic. In it we define the private field c and implement abstract methods getC() and setC() as access functions to this field. We define the functions f and g using lambda expressions, after which we check the possible cases of combination of coefficients. Due to the fact that some functions return the changed object (this), we create a chain of calls.
The source code of the AbstractQuadratic class can be as follows:
package ua.inf.iwanoff.quadratic.model;
import java.util.ArrayList;
import java.util.List;
public abstract class AbstractQuadratic {
private ExtendedFunction f;
private ExtendedFunction g;
private List<Double> roots = null;
public abstract double getC();
public abstract AbstractQuadratic setC(double c);
public AbstractQuadratic clearRoots() {
roots = null;
return this;
}
public ExtendedFunction getF() {
return f;
}
public AbstractQuadratic setF(ExtendedFunction f) {
this.f = f;
return clearRoots();
}
public ExtendedFunction getG() {
return g;
}
public AbstractQuadratic setG(ExtendedFunction g) {
this.g = g;
return clearRoots();
}
public AbstractQuadratic setABC(ExtendedFunction f, ExtendedFunction g, double c) {
this.f = f;
this.g = g;
setC(c);
return clearRoots();
}
public AbstractQuadratic solve(double t) {
roots = new ArrayList<>();
double a = f.applyAsDouble(t);
double b = g.applyAsDouble(t);
if (a == 0) {
if (b == 0 && getC() == 0) {
roots.add(null); // Infinity of roots
return this;
}
if (b == 0 && getC() != 0) {
return this; // No roots
}
roots.add(-getC() / b); // One root
return this;
}
// Calculation of discriminant:
double d = b * b - 4 * a * getC();
if (d < 0) {
return this; // No roots
}
roots.add((-b - Math.sqrt(d)) / (2 * a));
roots.add((-b + Math.sqrt(d)) / (2 * a));
return this;
}
public List<Double> getRoots() {
return roots == null ? null : new ArrayList<>(roots);
}
@Override
public String toString() {
if (getRoots() == null) {
return "The equation was not solved";
}
switch (getRoots().size()) {
case 0:
return "No roots";
case 1:
return getRoots().get(0) == null ? "Infinity of roots" : "Root: " + getRoots();
case 2:
return "Roots: " + getRoots();
}
return "Unknown error!";
}
public static void main(String[] args) throws Exception {
class TestQuadratic extends AbstractQuadratic {
private double c;
@Override
public double getC() {
return c;
}
@Override
public AbstractQuadratic setC(double c) {
this.c = c;
return clearRoots();
}
}
TestQuadratic quadratic = new TestQuadratic();
// The equation was not solved:
System.out.println(quadratic);
// General case:
System.out.println(quadratic.setF(x -> 1).setG(x -> -1).setC(-2).solve(0));
// Next, use the function setABC()
// No roots:
System.out.println(quadratic.setABC(x -> 1, x -> -1, 2).solve(0));
// Linear equation:
System.out.println(quadratic.setABC(x -> 0, x -> -2, 6).solve(0));
// No roots:
System.out.println(quadratic.setABC(x -> 0, x -> 0, 2).solve(0));
// Infinity of roots:
System.out.println(quadratic.setABC(x -> 0, x -> 0, 0).solve(0));
// Forgot to call solve():
System.out.println(quadratic.setF(x -> 1).setG(x -> 2).setC(3));
}
}
The results of the program can be as follows:
The equation was not solved Roots: [-1.0, 2.0] No roots Root: [3.0] No roots Infinity of roots The equation was not solved
Note: in the given implementation the work with the parameter t is not checked, because the functions selected for testing do not depend on it.
Now we can implement the functions f and g in accordance with the above problem. We create corresponding abstract classes. The AbstractFFunction class will represent the function f(t). When creating a class, we can immediately specify that it is abstract and implements the ExtendedFunction interface. The source code of the AbstractFFunction class can be as follows:
package ua.inf.iwanoff.quadratic.model;
public abstract class AbstractFFunction implements ExtendedFunction {
public abstract int aCount();
public abstract double getA(int i);
public abstract void setA(int i, double a);
public abstract void addA(double a);
@Override
public double applyAsDouble(double t) {
double product = 1;
for (int i = 0; i < aCount() - 1; i++) {
product *= getA(i) + getA(i + 1);
}
return product - t;
}
}
Similarly, we create an AbstractGFunction class:
package ua.inf.iwanoff.quadratic.model;
public abstract class AbstractGFunction implements ExtendedFunction {
public abstract int xyCount();
public abstract double getX(int i);
public abstract double getY(int i);
public abstract void setX(int i, double x);
public abstract void setY(int i, double y);
public abstract void addXY(double x, double y);
@Override
public double applyAsDouble(double t) {
double sum = 0;
for (int i = 0; i < xyCount(); i++) {
sum += getX(i) * getY(i);
}
return sum + t;
}
}
A class derived from AbstractFFunction uses an array to store the coefficients a. It will be called ArrayFFunction. It does not make sense to implement the method of adding and deleting coefficients. To prevent these methods from being accidentally called, we can place the UnsupportedOperationException standard exception in the body of the functions. In the main() function, we can test the function for argument values from a specified interval. The source code will be as follows:
package ua.inf.iwanoff.quadratic.model;
public class ArrayFFunction extends AbstractFFunction {
private double[] arr;
public ArrayFFunction(double... arr) {
this.arr = arr;
}
@Override
public int aCount() {
return arr.length;
}
@Override
public double getA(int i) {
return arr[i];
}
@Override
public void setA(int i, double a) {
arr[i] = a;
}
@Override
public void addA(double a) {
throw new UnsupportedOperationException();
}
@Override
public void deleteLast() {
throw new UnsupportedOperationException();
}
public static void main(String[] args) {
System.out.println(new ArrayFFunction(3, 1, 0, 0.25).test("t", "f", 0, 5, 1));
}
}
Similarly, we create an ArrayGFunction class. We can use two arrays to store pairs x and y. In the constructor we generate an exception if arrays have different length. The class code will be as follows:
package ua.inf.iwanoff.quadratic.model;
public class ArrayGFunction extends AbstractGFunction {
private double[] ax;
private double[] ay;
public ArrayGFunction(double[] ax, double[] ay) {
if (ax.length != ay.length) {
throw new RuntimeException("Wrong data");
}
this.ax = ax;
this.ay = ay;
}
@Override
public int xyCount() {
return ax.length;
}
@Override
public double getX(int i) {
return ax[i];
}
@Override
public double getY(int i) {
return ay[i];
}
@Override
public void setX(int i, double x) {
ax[i] = x;
}
@Override
public void setY(int i, double y) {
ay[i] = y;
}
@Override
public void addXY(double x, double y) {
throw new UnsupportedOperationException();
}
@Override
public void deleteLast() {
throw new UnsupportedOperationException();
}
public static void main(String[] args) {
System.out.println(new ArrayGFunction(new double[] { -1, 1, 0 } ,
new double[] { 2, 1, 1 }).test("t", "g", 0, 5, 1));
}
}
ArrayQuadratic class:
package ua.inf.iwanoff.quadratic.model;
public class ArrayQuadratic extends AbstractQuadratic {
private double c;
@Override
public double getC() {
return c;
}
@Override
public AbstractQuadratic setC(double c) {
this.c = c;
return clearRoots();
}
public ArrayQuadratic(ArrayFFunction f, ArrayGFunction g, double c) {
setF(f);
setG(g);
this.c = c;
}
public static void main(String[] args) {
ArrayQuadratic quadratic = new ArrayQuadratic(new ArrayFFunction(3, 1, 0, 0.25),
new ArrayGFunction(new double[] { -1, 1, 0 }, new double[] { 2, 1, 0.1 }), -2);
// The equation was not solved:
System.out.println(quadratic);
// General case:
System.out.println(quadratic.solve(0));
System.out.println(quadratic.solve(-5));
System.out.println(quadratic.solve(-10));
// No roots:
quadratic.setC(2);
System.out.println(quadratic.solve(0));
// Linear equation:
quadratic = new ArrayQuadratic(new ArrayFFunction(3, 0, 0, 0.25),
new ArrayGFunction(new double[] { -1, 0, 0 }, new double[] { 2, 1, 1 }), 6);
System.out.println(quadratic.solve(0));
// No roots:
quadratic = new ArrayQuadratic(new ArrayFFunction(3, 0, 0, 0.25),
new ArrayGFunction(new double[] { -1, 0, 0 }, new double[] { 0, 1, 1 }), 6);
System.out.println(quadratic.solve(0));
// Infinity of roots:
quadratic.setC(0);
System.out.println(quadratic.solve(0));
}
}
For data specified in the main() function, we will receive such an output on the console:
The equation was not solved Roots: [-1.0, 2.0] Roots: [-0.2637626158259733, 1.2637626158259734] Roots: [-0.15712874067277094, 1.157128740672771] No roots Root: [3.0] No roots Infinity of roots
3.3 Use of JAXB Technology
The created classes can now be used to implement an equation related to XML. Initially, the xml package should be added to the project structure, which will contain previously created document schema. When assuming that the generation of class mechanism has previously been added to IntelliJ IDEA, we can create EquationData and ObjectFactory classes that will be located in the xml package.
The XMLFFunction class:
package ua.inf.iwanoff.quadratic.model;
import ua.inf.iwanoff.quadratic.model.xml.EquationData;
import ua.inf.iwanoff.quadratic.model.xml.EquationData.ACoefs.ACoef;
public class XMLFFunction extends AbstractFFunction {
private EquationData data;
public XMLFFunction(EquationData data) {
this.data = data;
}
private EquationData.ACoefs aCoefs() {
if (data.getACoefs() == null) {
data.setACoefs(new EquationData.ACoefs());
}
return data.getACoefs();
}
@Override
public int aCount() {
return aCoefs().getACoef().size();
}
@Override
public double getA(int i) {
for (int j = 0; j < aCount(); j++) {
if (aCoefs().getACoef().get(j).getIndex() == i) {
return aCoefs().getACoef().get(j).getValue();
}
}
throw new RuntimeException("Wrong index");
}
@Override
public void setA(int i, double a) {
for (int j = 0; j < aCount(); j++) {
if (aCoefs().getACoef().get(j).getIndex() == i) {
aCoefs().getACoef().get(j).setValue(a);
}
}
throw new RuntimeException("Wrong index");
}
@Override
public void addA(double a) {
ACoef coef = new ACoef();
coef.setIndex(aCount());
coef.setValue(a);
aCoefs().getACoef().add(coef);
}
@Override
public void deleteLast() {
aCoefs().getACoef().remove(aCount() - 1);
}
}
The XMLGFunction class:
package ua.inf.iwanoff.quadratic.model;
import ua.inf.iwanoff.quadratic.model.xml.EquationData;
import ua.inf.iwanoff.quadratic.model.xml.EquationData.XYCoefs.XYCoef;
public class XMLGFunction extends AbstractGFunction {
private EquationData data;
public XMLGFunction(EquationData data) {
this.data = data;
}
private EquationData.XYCoefs aCoefs() {
if (data.getXYCoefs() == null) {
data.setXYCoefs(new EquationData.XYCoefs());
}
return data.getXYCoefs();
}
@Override
public int xyCount() {
return aCoefs().getXYCoef().size();
}
@Override
public double getX(int i) {
return aCoefs().getXYCoef().get(i).getX();
}
@Override
public double getY(int i) {
return aCoefs().getXYCoef().get(i).getY();
}
@Override
public void setX(int i, double x) {
aCoefs().getXYCoef().get(i).setX(x);
}
@Override
public void setY(int i, double y) {
aCoefs().getXYCoef().get(i).setY(y);
}
@Override
public void addXY(double x, double y) {
XYCoef coef = new XYCoef();
coef.setX(x);
coef.setY(y);
aCoefs().getXYCoef().add(coef);
}
@Override
public void deleteLast() {
aCoefs().getXYCoef().remove(xyCount() - 1);
}
}
The XMLQuadratic class:
package ua.inf.iwanoff.quadratic.model;
import java.io.*;
import javax.xml.bind.*;
import ua.inf.iwanoff.quadratic.model.xml.EquationData;
public class XMLQuadratic extends AbstractQuadratic {
public static class FileException extends Exception {
private String fileName;
public FileException(String fileName) {
this.fileName = fileName;
}
public String getFileName() {
return fileName;
}
}
public static class FileReadException extends FileException {
public FileReadException(String fileName) {
super(fileName);
}
}
public static class FileWriteException extends FileException {
public FileWriteException(String fileName) {
super(fileName);
}
}
private EquationData data;
public XMLQuadratic() {
clearEquation();
}
public XMLQuadratic(String fileName) {
try {
readFromFile(fileName);
}
catch (FileReadException ex) {
throw new RuntimeException("Error reading " + fileName);
}
}
public XMLQuadratic clearEquation() {
clearRoots();
data = new EquationData();
setF(new XMLFFunction(data));
setG(new XMLGFunction(data));
return this;
}
@Override
public double getC() {
return data.getCCoef();
}
@Override
public AbstractQuadratic setC(double c) {
data.setCCoef(c);
return clearRoots();
}
public EquationData getData() {
return data;
}
public AbstractFFunction getFFunction() {
return (AbstractFFunction) getF();
}
public AbstractGFunction getGFunction() {
return (AbstractGFunction) getG();
}
public XMLQuadratic readFromFile(String fileName) throws FileReadException {
try {
JAXBContext jaxbContext = JAXBContext.newInstance("ua.inf.iwanoff.quadratic.model.xml");
Unmarshaller unmarshaller = jaxbContext.createUnmarshaller();
data = (EquationData) unmarshaller.unmarshal(new FileInputStream(fileName));
setF(new XMLFFunction(data));
setG(new XMLGFunction(data));
return this;
}
catch (FileNotFoundException | JAXBException e) {
throw new FileReadException(fileName);
}
}
public XMLQuadratic writeToFile(String fileName) throws FileWriteException {
try {
JAXBContext jaxbContext = JAXBContext.newInstance("ua.inf.iwanoff.quadratic.model.xml");
Marshaller marshaller = jaxbContext.createMarshaller();
marshaller.setProperty(Marshaller.JAXB_FORMATTED_OUTPUT, Boolean.TRUE);
marshaller.marshal(data, new FileWriter(fileName));
return this;
}
catch (IOException | JAXBException e) {
throw new FileWriteException(fileName);
}
}
public XMLQuadratic saveReport(String fileName, String imageName, double t) throws FileWriteException {
try (PrintWriter out = new PrintWriter(
new OutputStreamWriter(new FileOutputStream(fileName), "UTF-8"))) {
out.printf("<html>%n");
out.printf("<head>%n");
out.printf("<meta http-equiv='Content-Type' content='text/html; " +
"charset=UTF-8'>%n");
out.printf("</head>%n");
out.printf("<body>%n");
out.printf("<h2>Report</h2>%n");
out.printf("<p>As a result of solving the following solution, with such input data:</p>%n");
out.printf("<h4>Data for the function <span style='font-family:Times, Serif;'>" +
"<em>f(t)</em></span></h4>%n");
out.printf("<table border = '1' cellpadding=4 cellspacing=0>%n");
out.printf("<tr>%n");
out.printf("<th>Index</th>%n");
out.printf("<th>a</th>%n");
out.printf("</tr>%n");
out.printf("<td>%n");
for (int i = 0; i < getFFunction().aCount(); i++) {
out.printf("<tr>%n");
out.printf("<td>%d</td>", i);
out.printf("<td>%8.3f</td>%n", getFFunction().getA(i));
out.printf("</tr>%n");
}
out.printf("</table>%n");
out.printf("<h4>Data for the function <span style='font-family:Times, Serif;'>" +
"<em>g(t)</em></span></h4>%n");
out.printf("<table border = '1' cellpadding=4 cellspacing=0>%n");
out.printf("<tr>%n");
out.printf("<th>Index</th>%n");
out.printf("<th>x</th>%n");
out.printf("<th>y</th>%n");
out.printf("</tr>%n");
out.printf("<td>%n");
for (int i = 0; i < getGFunction().xyCount(); i++) {
out.printf("<tr>%n");
out.printf("<td>%d</td>", i);
out.printf("<td>%8.3f</td>%n", getGFunction().getX(i));
out.printf("<td>%8.3f</td>%n", getGFunction().getY(i));
out.printf("</tr>%n");
}
out.printf("</table>%n");
out.printf("<p>The value of the parameter <em>t</em>: %8.3f</p>%n", t);
solve(t);
switch (getRoots().size()) {
case 0:
out.printf("<p>it was found that the equation has no roots.%n</p>");
break;
case 1:
if (getRoots().get(0) == null) {
out.printf("<p>it was found that the equation has infinite count of roots.</p>%n");
}
else {
out.printf("<p>such a root was obtained: %s</p>%n", getRoots().get(0));
}
break;
case 2:
out.printf("<p>the following roots were obtained:</p>%n");
for (Double root : getRoots()) {
out.printf("%8.3f<br>%n", root);
}
break;
default:
throw new RuntimeException("Unknown error");
}
if (imageName != null) {
out.printf("<img src = \"" + imageName + "\"/>");
}
out.printf("</body>%n");
out.printf("</html>%n");
return this;
}
catch (IOException e) {
throw new FileWriteException(fileName);
}
}
}
The ConsoleApp class demonstrates how the program works:
package ua.inf.iwanoff.quadratic.model;
import ua.inf.iwanoff.quadratic.model.XMLQuadratic.FileException;
public class ConsoleApp {
public static void main(String[] args) throws FileException {
XMLQuadratic quadratic = new XMLQuadratic("EquationCommon.xml");
// The equation was not solved:
System.out.println(quadratic);
// General case:
System.out.println(quadratic.solve(0));
System.out.println(quadratic.solve(-5));
System.out.println(quadratic.solve(-10));
quadratic.saveReport("Common.html", null, -10);
// No roots:
System.out.println(quadratic.readFromFile("EquationNoSolutions.xml").solve(0));
quadratic.saveReport("NoSolutions.html", null, 0);
// Linear equation:
System.out.println(quadratic.readFromFile("LinearEquation.xml ").solve(0));
quadratic.saveReport("Linear.html", null, 0);
// No roots:
System.out.println(quadratic.readFromFile("LinearEquationNoSolutions.xml").solve(0));
quadratic.saveReport("NoSolutions.html", null, 0);
// Infinity of roots:
quadratic.setC(0);
System.out.println(quadratic.solve(0));
quadratic.writeToFile("Infinity.xml");
quadratic.saveReport("Infinity.html", null, 0);
// Create an equation "from scratch":
quadratic.clearEquation();
quadratic.getFFunction().addA(1);
quadratic.getFFunction().addA(0);
quadratic.getGFunction().addXY(1, 2);
quadratic.setC(1);
System.out.println(quadratic.solve(0));
}
}