Лабораторна робота 3
Використання функцій
1 Завдання на лабораторну роботу
1.1 Статичні локальні змінні
Написати програму, яка обчислює та виводить мінімум і максимум цілих чисел, в міру того, як користувач вводить ці числа. Слід використати статичні локальні змінні.
1.2 Рекурсія
Написати програму, яка зчитує x і n і обчислює y за допомогою рекурсивної функції:
1.3 Аргументи з усталеними значеннями
Створити функції, які повертають 1, аргумент, і добуток аргументів, залежно від кількості аргументів. Першу
функцію реалізувати з усталеними значеннями аргументів, інші функції – через механізм перевантаження імен.
У функції main() слід здійснити тестування всіх функцій.
1.4 Квадратне рівняння
Створити функцію для розв'язання квадратного рівняння. Функція повинна повертати кількість коренів (0, 1 або 2) або -1, якщо рівняння має безліч розв'язків. Функція повинна отримати коефіцієнти як аргументи та повертати корені як аргументи-посилання.
1.5 Індивідуальне завдання
Створити програму, яка реалізує індивідуальне завдання попередньої лабораторної
роботи. Програма повинна бути розділена на декілька функцій. Функція y() повинна отримувати
значення x і n як аргументи і повертати значення, розраховані за формулою, наведеною в
індивідуальному завданні. Створити окрему функцію для зчитування даних. Не використовувати глобальні змінні.
2 Методичні вказівки
2.1 Оголошення та визначення функції
Функція (function) – це підпрограма, яка може отримати дані та повертати деяке значення. Кожна функція має своє власне ім'я. Коли це ім'я зі списком даних (параметрів) зустрічається будь-де у програмі, виконання програми переходить до тіла цієї функції. Такий перехід має назву виклику функції (function call). Після того, як були виконані інструкції в тілі функції, процес виконання повертається до попередньої функції (з якої було здійснено виклик) та виконуються її наступні інструкції. Складні програми повинні бути розділені на декілька функцій, виклик яких здійснюється по черзі.
Виклик функції main() здійснюється операційною системою.
Під час виклику функцій усі їх локальні змінні, адреси функцій, а також значення параметрів і інші локальні дані розміщуються в спеціальній області пам'яті, що зветься програмним стеком, або стеком викликів (call stack). Під час повернення з функції область, зайнята її локальними даними, звільняється.
Визначення функції включає тіло функції - блок з програмним кодом, який виконується під
час виклику функції.
Оголошення функції без визначення має назву прототипу (prototype). Прототип функції складається з типу результату функції, імені та списку параметрів. Список параметрів (parameter list) – це список всіх аргументів та їх типів, розділених комами.
int sum(int a, int b); // прототип
Прототип функції та визначення функції повинні збігатися щодо типу результату, імені та списку параметрів. Прототип функції не обов'язково містить імена параметрів:
int sum(int, int); // прототип
Визначення функції (function definition) складається з заголовка функції й тіла. Тіло функції (function body) – це набір інструкцій, укладених у фігурні дужки.
int sum(int a, int b)
{
return a + b;
}
Усі функції мають тип результату.
Інструкція return завершує виконання функції та повертає управління до
попередньої функції, з якої було здійснено виклик. Інструкція return всередині
функції main() передає управління операційній системі, а результат, який повертає функція main(),
може бути використаний як код помилки (0 - помилок немає).
Значення виразу в інструкції return повертається до функції, з якої було
здійснено виклик. Функції усіх типів (за винятком void) повинні містити інструкцію
return з таким виразом.
Інструкція return завжди завершує виконання функції.
Функцію не можна визначити всередині іншої функції. У C++ немає локальних функцій.
Незважаючи на те, що немає обмеження на розмір функції, добре спроєктовані функції зазвичай містять не дуже багато коду. Функцію з меншим розміром легше зрозуміти та підтримувати її роботу.
Аргументи передаються у функцію в тому порядку, в якому вони були оголошені й визначені. Будь-який вираз C++ може бути аргументом функції, в тому числі константа, математичні та логічні вирази, виклик інших функцій, які повертають значення.
int main()
{
int x, y;
cin >> x >> y;
int z = sum(x, y); // виклик функції
int k = sum(z, x + y); // виклик функції
int m = sum(k, sum(x + y, z)); // виклик функції
cout << z << ' ' << k << ' ' << m;
return 0;
}
Аргументи, передані у функцію, є локальними для функції. Зміни значень аргументів всередині викликаної функції не впливають на значення в функції, з якої було здійснено виклик. Це відомо як передача за значенням і означає, що у функції створена локальна копія кожного аргументу.
Аргументи, які передаються під час виклику функції, мають назву фактичних параметрів. Викликана функція має доступ до переданої інформації через так звані формальні параметри.
2.2 Тип void
Якщо функція не повертає ніяких значень, її тип повинен бути void.
void print(double a)
{
cout << a << endl;
}
Тип void синтаксично є фундаментальним типом. Він може, однак, бути використаний тільки як
частина більш складного типу; немає об'єктів типу void.
У тілі функції з типом результату void інструкція return може
бути відсутня: тіло функції виконується до кінця програмного блоку. Якщо інструкція return
присутня, то після її не повинно бути ні якого виразу. Інструкцію return можна
використовувати для дострокового повернення з функції. Наприклад:
void printReciprocal(double a)
{
if (a == 0)
{
return;
}
cout << 1 / a << endl;
}
Функцію з типом результату void можна викликати тільки окремою інструкцією (не
всередині виразу).
2.3 Область видимості
Кожен програмний об'єкт, зокрема змінна, має свою область видимості, яка визначає, де саме в програмі цей об'єкт може бути доступний.
Змінні можна створити всередині тіла функції, або іншого програмного блоку. Такі змінні є локальними змінними. Вони існують тільки всередині функції під час її виконання. Формальні параметри також є локальними змінними.
Глобальні змінні мають глобальну область видимості. Вони доступні в будь-якому місці програми.
Глобальні змінні, визначені поза тілом функції, доступні з будь-якої функції в програмі, у тому числі з функції
main(). Локальні змінні з тим же ім'ям, що й глобальні змінні, не пов'язані з відповідними
глобальними змінними. Але локальна змінна з таким же ім'ям, як і глобальна змінна, приховує глобальну
змінну. В таких випадках для доступу до глобальної змінної використовують операцію доступу до області
видимості :: (scope resolution operator). Наприклад:
int k = 1;
void f()
{
int k = 2;
cout << k; // 2
cout << ::k; // 1
}
Синтаксис мови C++ дозволяє використовувати глобальні змінні, їх використання є небажаним. Глобальні змінні створюють небезпеку, оскільки вони є спільними даними. Будь-яка функція може змінити значення глобальної змінної, після чого інша функція, в якій передбачено використання певного значення глобальної змінної, може неправильно виконуватися. Такі помилки дуже важко знаходити.
2.4 Статичні локальні змінні
Як правило, локальні змінні, створені у функції, зникають після виходу з функції. Коли виклик функції
здійснюється знову, зміні створюються та ініціалізуються заново. Якщо треба, щоб дані зберігалися протягом
усього життєвого циклу програми, така змінна може бути визначена як статична (з модифікатором static).
Ініціалізація виконується тільки тоді, коли функція викликається вперше, а змінні зберігають свої значення
проміж викликами функції. Наведений нижче приклад демонструє відмінність між звичайними (автоматичними) і
статичними локальними змінними:
#include <iostream>
using namespace std;
void localVariables()
{
int m = 0;
static int n = 0;
m++;
n++;
cout << m << " " << n << endl;
}
int main()
{
localVariables(); // 1 1
localVariables(); // 1 2
localVariables(); // 1 3
return 0;
}
Не зважаючи на те, що статичні змінні існують протягом життєвого циклу програми, не існує механізмів доступу до таких змінних ззовні функції. Це зменшує ймовірність помилок.
2.5 Рекурсія
Функція може викликати себе. Такий механізм має назву рекурсії.
Рекурсія може бути безпосередньою або опосередкованою. Безпосередня рекурсія передбачає виклик функції безпосередньо з цієї функції:
void f() {
...
f();
...
}
Опосередкована передбачає, що перша функція викликає другу, а потім друга викликає першу функцію. В цьому випадку обов'язково необхідно створити прототип принаймні однієї з функцій:
void f(); // прототип
void g() {
...
f();
...
}
void f() {
...
g();
...
}
Важливо відзначити, що коли функція викликає саму себе, створюється нова копія даних цієї функції. Локальні змінні в новій копії не залежать від локальних змінних попередньої копії.
Неправильне вживання рекурсії може призвести до переповнення стеку викликів.
Іноді рекурсія може бути використана замість циклу. Наприклад, можна обчислити суму
взагалі без циклів:
#include <iostream>
using namespace std;
double sum(int n)
{
if (n <= 1)
{
return 1;
}
else
{
return n * n + sum(n - 1);
}
}
int main()
{
cout << sum(5);
return 0;
}
2.6 Функції-підстановки
Коли здійснюється виклик функції, виконання програми переходить до відповідної групи інструкцій. Коли виконання функції завершується, виконання переходить назад на наступний рядок функції, з якої було здійснено виклик. Ці дії можуть бути пов'язані з деяким зниженням ефективності виконання.
Існують так звані функції-підстановки, або вбудовані. Такі функції мають модифікатор
inline:
inline int min(int a, int b)
{
return a < b ? a : b;
}
Якщо функція оголошена як вбудована, компілятор підставляє в точку виклику її тіло. Доцільно з модифікатором
inline описувати найпростіші функції, багаторазове підставляння яких не істотно вплине на
розміри програми.
Функція-підстановка не може бути рекурсивною.
2.7 Перевантаження імен функцій
Мова C++ дозволяє створити декілька функцій з однаковими іменами. Це називається перевантаженням імен функцій (function name overloading). Перевантажені функції дозволяють програмістам реалізувати різну семантику для функції, залежно від типів і кількості аргументів.
Функції повинні відрізнятися списками параметрів: різними типами параметрів, різним числом параметрів, або обома ознаками. Наприклад:
int sum(int a, int b)
{
return a + b;
}
double sum(double a, double b)
{
return a + b;
}
double sum(double a, double b, double c)
{
return a + b + c;
}
int main()
{
cout << sum(1, 2) << endl; // перша функція sum()
cout << sum(1.0, 2.5) << endl; // друга функція sum()
cout << sum(1, 2, 2.6) << endl; // третя функція sum()
return 0;
}
Примітка: дві функції з однаковим ім'ям і списком параметрів, але з різними типами результату, генерують помилку компіляції:
int f(double x); double f(double x); // Помилка!
2.8 Усталені значення аргументів
У багатьох випадках для аргументів функції можна вказати усталені значення (default values), які можуть бути цілком задовільними в багатьох випадках. Для розв'язання цієї проблеми реалізовано механізм аргументів з усталеними значеннями, що дозволяє визначати лише ті аргументи функції, які є істотними в конкретному контексті. Наприклад:
int sum(int x, int y = 0, int z = 0)
{
return x + y + z;
}
int main()
{
cout << sum(5) << endl; // 5, y = 0, z = 0
cout << sum(1, 2) << endl; // 3, z = 0
cout << sum(1, 2, 5) << endl; // 8
return 0;
}
Аргументи з усталеними значеннями використовують у випадках, коли параметри в кінці списку можуть бути відсутні. Усі параметри функції можуть бути з усталеними значеннями. Слід пам'ятати, що аргументи з усталеними значеннями повинні бути останніми в списку:
void f(double x, int y = 0, int h); // помилка
Усталене значення не може бути повторене в більш пізніх описах функції, навіть якщо перевизначення ідентичне оригіналу. Таким чином, наведений нижче код видає помилку:
void f(double x, int y = 1);
void f(double x, int y = 1) { } // помилка
// Слід писати void f(double x, int y) { }
2.9 Посилання
У мові C++ визначено механізм створення так званих посилань. Посилання (reference) може бути визначене як друге ім'я (псевдонім) існуючої змінної (об'єкта).
Можна описати посилання зазначенням типу, за яким слідує оператор посилання (&) та ім'я посилання:.
int i = 10; int &j = i; // посилання на i j = 11; cout << i; // 11
Не можна створювати посилання, не вказуючи об'єкт, на який ми посилаємось. Посилання повинні бути ініціалізовані під час створення:
int &k; // синтаксична помилка!
Можна визначити посилання на константний об'єкт:
int m = 2; const int &n = m; // посилання на i double x = n + 1; // OK m = 11; // OK n = 12; // помилка!
Посилання можуть бути використані як аргументи функції. Наприклад, можна створити функцію, яка обмінює значення двох цілих змінних:
void swap(int &x1, int &x2)
{
int x = x1;
x1 = x2;
x2 = x;
}
Тепер функцію swap() можна викликати з функції main():
void main()
{
int a = 1;
int b = 2;
swap(a, b);
cout << a << endl; // 2
cout << b << endl; // 1
}
Посилання можуть бути використані як тип результату функції. Дуже важливо бути впевненим, що посилання пов'язане зі змінною, яка існує після виходу з функції:
int& f()
{
int k;
return k; // Помилка; k знищується після виходу з функції
}
А це правильно:
int& f()
{
static int k;
return k; // OK
}
void main()
{
f() = 10;
cout << f(); // 10
}
Функція повертає псевдонім статичної змінної, яка не знищується після виходу з функції. Таким чином, ми можемо здійснити таке присвоєння:
f() = 10;
3 Приклади програм
3.1 Сума послідовних степенів числа
У наведеній нижче програмі вводиться величина x і ціле значення n. Необхідо обчислити
суму послідовних цілих степенів x від 1 до n.
#include <iostream>
using namespace std;
double sumOfPowers(double x, int n)
{
double sum = 0;
double power = 1;
// Степені та суму можна розрахувати за один цикл:
for (int i = 0; i < n; i++)
{
power *= x;
sum += power;
}
return sum;
}
int main()
{
double x;
int n;
cout << "Enter x and n:";
cin >> x >> n;
cout << sumOfPowers(x, n);
return 0;
}
3.2 Статичні локальні змінні
У наведеній нижче програмі обчислюється сума цілих значень які вводить користувач:
#include <iostream>
using namespace std;
int add(int i)
{
static int sum = 0;
sum += i;
return sum;
}
int main()
{
int i;
do
{
cin >> i;
cout << add(i) << endl;
}
while (i);
return 0;
}
3.3 Поділ програми на незалежні частини
Майже всі програми можна розділити на відносно незалежні частини. Програма, яка обчислює деякі значення, як правило, містить частини, відповідальні за введення, розрахунки і виведення. Припустимо, що нам необхідно реалізувати програму, яка обчислює суму квадратів цілих чисел:
Перша реалізація не поділена на частини:
#include <iostream>
using namespace std;
int main()
{
int n;
cout << "Input n:";
cin >> n;
int y = 0;
for (int i = 1; i <= n; i++)
{
y += i * i;
}
cout << "y = " << y;
return 0;
}
Найпростіше рішення полягає у використанні глобальних змінних:
#include <iostream>
using namespace std;
int n;
int y = 0;
void read()
{
cout << "Input n:";
cin >> n;
}
void calc()
{
for (int i = 1; i <= n; i++)
{
y += i * i;
}
}
void write()
{
cout << "y = " << y;
}
int main()
{
read();
calc();
write();
return 0;
}
Використання глобальних змінних не є гарною ідеєю. Кращий підхід полягає у використанні параметрів:
#include <iostream>
using namespace std;
int read()
{
int n;
cout << "Input n:";
cin >> n;
return n;
}
int calc(int n)
{
int y = 0;
for (int i = 1; i <= n; i++)
{
y += i * i;
}
return y;
}
void write(int y)
{
cout << "y = " << y;
}
int main()
{
int n = read();
int y = calc(n);
write(y);
return 0;
}
Функція main() може бути реалізована взагалі без змінних:
...
int main()
{
write(calc(read()));
return 0;
}
3.4 Лінійне рівняння
Функція solve() в наведеному нижче прикладі знаходить корінь лінійного рівняння (аргумент, який
передається за посиланням) i повертає кількість коренів. Якщо коренів безмежна кількість, функція повертає -1.
Всередині функції main() доцільно створити перемикач, який аналізує кількість розв'язків і здійснює
відповідні виведення.
#include <iostream>
using namespace std;
int solve(double a, double b, double& x)
{
if (a == 0)
{
if (b == 0)
{
return -1;
}
else
{
return 0;
}
}
x = -b / a;
return 1;
}
int main()
{
setlocale(LC_ALL, "UKRAINIAN");
double a, b, x;
cin >> a >> b;
int count = solve(a, b, x);
switch (count)
{
case -1:
cout << "Безмежна кiлькiсть розв'язкiв";
break;
case 0:
cout << "Немає розв'язкiв";
break;
case 1:
cout << "x = " << x;
}
cout << endl;
return 0;
}
3.5 Таблиця значень функції
Припустимо, необхідно створити програму, яка на заданому діапазоні з певним кроком обчислює значення функції
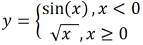
Окремі частини програми доцільно реалізувати як незалежні функції. Програма може бути такою:
#include <iostream>
#include <cmath>
using namespace std;
// функція введення даних з клавіатури, параметри передаються за посиланням
bool readData(double& from, double& to, double& step)
{
cout << "Введiть початок, кiнець iнтервалу та крок: ";
cin >> from >> to >> step;
if (from >= to || step <= 0)
{
cerr << "Wrong data" << endl;
return false;
}
return true;
}
// Функція, визначена в завданні
double y(double x)
{
if (x < 0)
{
return sin(x);
}
else
{
return sqrt(x);
}
}
// Виведення значень аргументів і функції на інтервалі з визначеним кроком
void printInALoop(double from, double to, double step)
{
cout << "x\ty" << endl; // "шапка" таблиці
for (double x = from; x <= to; x += step)
{
cout << x << "\t" << y(x) << endl;
}
}
int main()
{
setlocale(LC_ALL,"UKRAINIAN");
double from, to, step;
if (readData(from, to, step))
{
printInALoop(from, to, step);
return 0; // таблицю виведено
}
return -1; // помилка введення даних
}
Розташування функцій у програмі визначається механізмом виклику. Функція, яка викликається, повинна передувати функції, яка її викликає. Такий порядок не завжди зручний з точки зору сприйняття коду людиною. Якщо спочатку розташувати прототипи функцій, порядок можна змінити:
#include <iostream>
#include <cmath>
using namespace std;
// Прототипи функцій:
bool readData(double &, double &, double &);
void printInALoop(double, double, double);
double y(double);
int main()
{
double from, to, step;
if (readData(from, to, step))
{
printInALoop(from, to, step);
return 0; // таблицю виведено
}
return -1; // помилка введення даних
}
// функція введення даних з клавіатури, параметри передаються за посиланням
bool readData(double& from, double& to, double& step)
{
cout << "Введiть початок, кiнець iнтервалу та крок: ";
cin >> from >> to >> step;
if (from >= to || step <= 0)
{
cerr << "Wrong data" << endl;
return false;
}
return true;
}
// Виведення значень аргументів і функції на інтервалі з визначеним кроком
void printInALoop(double from, double to, double step)
{
cout << "x\ty" << endl; // "шапка" таблиці
for (double x = from; x <= to; x += step)
{
cout << x << "\t" << y(x) << endl;
}
}
// Функція, визначена в завданні
double y(double x)
{
if (x < 0)
{
return sin(x);
}
else
{
return sqrt(x);
}
}
4 Вправи для контролю
- Створити програму для тестування функції
signum() - Здійснити розробку та тестування функції, яка обчислює добуток трьох аргументів
- Здійснити розробку та тестування функції, яка обчислює добуток перших n непарних значень
- Здійснити розробку та тестування функції, яка обчислює ex через суму
- Здійснити розробку та тестування функції, яка обчислює факторіал
- Здійснити розробку та тестування функції, яка здійснює виведення всіх парних значень в заданому діапазоні
- Здійснити розробку та тестування функції, яка здійснює виведення добутку перших n парних значень
- Здійснити розробку та тестування функції, яка обчислює найбільший спільний дільник двох цілих чисел
5 Контрольні запитання
- Що таке функція?
- Що таке заголовок функції?
- Що таке тіло функції?
- Що таке прототип функції?
- Чи є імена формальних параметрів завжди обов'язковими в заголовку функції?
- Як створити локальну функцію?
- Як здійснюється передача параметрів у функцію?
- У чому різниця між формальними і фактичними параметрами?
- Чи є інструкція return завжди обов'язковою?
- Як використовувати результат функції з типом результату void?
- Що таке локальна змінна?
- Що таке область видимості (scope)?
- Що таке глобальна область видимості?
- Як отримати доступ до імен з глобальної області видимості?
- Чи можуть локальні змінні приховати глобальні змінні?
- У чому різниця між статичними і нестатичними локальними змінними?
- Яким є життєвий цикл статичної локальної змінної?
- Як використовують статичні локальні змінні?
- Що таке рекурсія?
- Що таке функція-підстановка (inline)?
- Як перевантажити ім'я функції?
- Чи можна створити дві глобальні функції з однаковими іменами і списками параметрів, але з різними типами результату?
- Як описати аргументи з усталеними значеннями?
- Що таке посилання?
- Як ініціалізувати посилання?
- Для чого використовують посилання?
- Чи можна повернути посилання з функції?
- Чи можна повертати посилання на нестатичну локальну змінну?
